1. Таблица с исходным данными, включающая: название страны (РФ), факторный (Уровень заболеваемости (на 1000 человек населения)), результативный (Ожидаемая продолжительность жизни) признак и признак для выполнения п. 3 (Уровень заболеваемости (на 1000 человек населения): болезни органов дыхания).
Название региона Уровень заболеваемости (на 1000 человек населения) Ожидаемая продолжительность жизни при рождении всего Уровень заболеваемости (на 1000 человек населения): болезни органов дыхания Российская Федерация
744,90
65,07 294,00
Центральный ф. д.
720,90
65,81
318,40
Белгородская область 806,10 68,26 271,30 Брянская область 741,80 64,62 299,60 Владимирская область 920,90 63,18 399,30 Воронежская область 548,30 66,19 210,10 Ивановская область 850,60 62,42 394,30 Калужская область 816,30 64,56 342,00 Костромская область 692,80 62,39 321,20 Курская область 649,60 65,35 240,80 Липецкая область 714,20 65,85 318,80 Московская область 624,90 65,26 307,00 Орловская область 821,70 65,23 304,10 Рязанская область 641,60 63,91 245,50 Смоленская область 777,20 62,34 331,80 Тамбовская область 721,10 65,47 310,60 Тверская область 754,10 61,53 339,60 Тульская область 822,70 63,03 372,00 Ярославская область 937,00 63,46 398,40 г. Москва 711,70 69,64 333,60 Северо-Западный ф. о.
749,90
63,43
313,60
Республика Карелия 1057,30 60,81 437,70 Республика Коми 984,80 61,67 439,80 Архангельская область 930,30 62,11 384,80 Вологодская область 808,20 62,47 369,50 Калининградская область 668,90 61,68 255,30 Ленинградская область 524,70 61,74 232,30 Мурманская область 817,30 63,2 351,30 Новгородская область 817,40 60,84 348,20 Псковская область 606,10 60,86 276,20 г. Санкт-Петербург 682,80 66,49 266,60 Южный ф.а.
651,80
67,49
237,00
Республика Адыгея 657,80 67,51 199,00 Республика Дагестан 844,80 72,33 230,40 Республика Ингушетия 485,80 75,13 130,30 Кабардино-Балкарская Республика 354,40 68,7 120,60 Республика Калмыкия 688,80 66,18 317,50 Карачаево-Черкесская Республика 506,20 68,1 180,60 Республика Северная Осетия — Алания 569,50 68,47 203,20 Чеченская Республика … 69,06 … Краснодарский край 570,30 67,33 202,90 Ставропольский край 485,50 67,14 223,30 Астраханская область 728,60 65,36 274,00 Волгоградская область 776,20 66,43 288,70 Ростовская область 776,20 66,47 294,90 Приволжский ф.а.
799,60
65,29
303,10
Республика Башкортостан 797,60 66,39 277,40 Республика Марий Эл 768,30 63,99 265,00 Республика Мордовия 696,80 66,28 235,50 Республика Татарстан 760,80 67,84 276,70 Удмуртская Республика 912,80 64,34 396,00 Чувашская Республика 820,90 66,09 274,00 Кировская область 706,30 63,71 307,90 Нижегородская область 762,40 64,03 317,20 Оренбургская область 908,50 65,35 308,00 Пензенская область 852,10 65,67 317,90 Пермская область 834,30 62,31 330,00 Самарская область 844,00 65,59 335,70 Саратовская область 675,70 65,46 263,10 Ульяновская область 877,10 65,25 320,40 Уральский ф. о.
774,10
64,79
304,80
Курганская область 843,10 63,87 272,30 Свердловская область 685,80 63,97 275,20 Тюменская область 897,30 66,07 350,90 Челябинская область 750,60 64,78 308,30 Сибирский ф. о.
776,60
63,17
274,40
Республика Алтай 876,70 60,24 242,40 Республика Бурятия 610,70 61,25 213,80 Республика Тыва 637,30 54,31 189,20 Республика Хакасия 783,70 60,75 239,40 Алтайский край 969,90 66,05 326,20 Красноярский край 759,20 63,03 261,70 Иркутская область 837,80 60,68 312,10 Кемеровская область 741,70 61,86 267,70 Новосибирская область 685,90 65,83 270,00 Омская область 830,40 66,01 300,00 Томская область 764,10 64,44 229,50 Читинская область 620,30 60,24 224,40 Дальневосточный ф. о.
758,60
62,42
292,30
Республика Саха (Якутия) 847,70 63,96 326,60 Приморский край 727,90 63,07 269,90 Первый конец 715,90 61,85 289,60 Амурская область 617,60 61,26 242,90 Камчатская область 866,00 63 357,50 Магаданская область 942,60 63,03 372,80 Сахалинская область 932,10 61,44 333,20 Еврейская автономная область 620,30 60,8 215,10 Чукотский автономный округ 1296,80 59,1 620,30 Уровень заболеваемости населения — отношение числа больных с впервые в жизни установленным диагнозом к среднегодовой численности населения.
Ожидаемая продолжительность жизни при рождении — число лет, которое в среднем предстояло бы прожить одному человеку из некоторого гипотетического поколения родившихся при условии, что на протяжении всей жизни этого поколения уровень смертности в каждом возрасте останется таким, как в годы, для которых вычислен показатель. Ожидаемая продолжительность жизни является наиболее адекватной обобщающей характеристикой современного уровня смертности во всех возрастах.
2. Аналитическая группировка, характеризующая зависимость между факторным и результативным признаком
Таблица 1
Уровень заболеваемости (на 1000 человек) Число регионов, входящих в группу Численность населения Средняя ожидаемая продолжительность жизни при рождении Общая продолжительность жизни при рождение Изменение средней ожидаемой жизни при рождение по сравнению с группой с минимальной ожидаемой продолжительностью жизни при рождение 485,5-624,9 12 23973,4 64,91 843,77 118,2 624,9-696,8 10 20281,1 64,11 769,36 129,0 696,8-760,8 11 34529,2 64,51 838,61 139,4 760,8-820,9 12 24452,0 64,30 900,26 148,0 820,9-866 10 20481,7 64,51 774,1 164,4 866-1057,3 11 17667,9 63,31 823 75,0 Итого: 66 141385,3 385,65 4949,1 774,0
№ группы
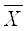

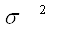
V Выводы об однородности данных в группах 1 64,91 4,22 17,83 6,50% Коэффициент вариации V=σ/x * 100% < 17% следовательно данные совершенно однородны 2 64,11 3,39 11,46 5,28% 3 64,51 2,30 5,29 3,57% 4 64,30 2,17 4,70 3,37% 5 64,51 2,82 7,96 4,37% 6 63,31 1,91 3,66 3,02% 385,65
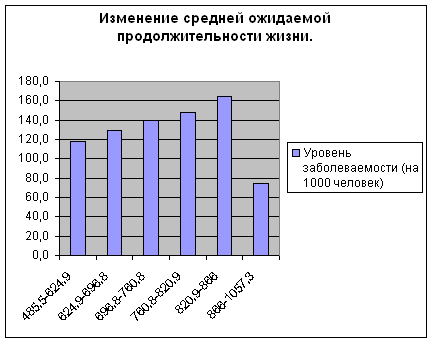
Вывод: Таблица №1 отражает определенную зависимость между уровнем заболеваемости и ожидаемой продолжительностью жизни при рождение всего, зависимость прямая и так как количество регионов в группе сопоставимо (данные однородны).
3. Аналитическая группировка, характеризующая зависимость между территориальным и результативным признаком
Таблица 2
Название федерального округа Кол-во регионов Численность населения Средняя продолжительность жизни при рождении Изменение средней ожидаемой жизни при рождение по сравнению с группой с минимальной ожидаемой продолжительностью жизни при рождение Центральный 17 37545,8 64,59 104,3 Северо-Западный 10 13731 62,19 100,4 Южный 13 22820,8 68,26 110,2 Приволжский 14 30710,2 65,16 105,2 Уральский 4 12279,2 64,67 104,4 Сибирский 12 19794,2 62,06 100,2 Дальневосточный 9 6593 61,95 103,5 Итого: 79 143474,2 448,89 728,2
№ группы

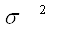
V Выводы об однородности данных в группах 1 64,59 2,05 4,19 3,17% Коэффициент вариации V=σ/x * 100% < 17% следовательно данные совершенно однородны 2 62,19 1,61 2,58 2,58% 3 68,26 2,58 6,66 3,78% 4 65,16 1,33 1,78 2,05% 5 64,67 0,88 0,78 1,36% 6 62,06 3,21 10,28 5,17% 7 61,95 1,40 1,97 0,02%

4. Построить вариационный ряд, характеризующий распределение регионов(стран) по величине признака, указанного в варианте (Уровень заболеваемости (на 1000 человек населения) болезни органов дыхания)
Группа регионов по уровню заболеваемости (на 1000 человек населения): болезни органов дыхания% Число регионов в группе Среднее значение исследуемого признака 1 180,6 230,4 12 210,125 2 230,4 266,6 12 249,208 3 266,6 277,4 11 273,155 4 277,4 317,2 14 303,692 5 317,2 348,2 14 328,179 6 348,2 439,8 14 383,750 Итого: 77 Анализ однородности данных в группах
№ группы
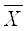

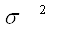
V Выводы об однородности данных в группах 1 210,13 15,10 227,97 7,19% Коэффициент вариации V=σ/x * 100% < 17% следовательно данные совершенно однородны 2 249,21 11,83 139,88 4,75% 3 273,16 3,01 9,09 1,10% 4 303,69 8,32 69,27 2,74% 5 328,18 3,02 9,12 0,92% 6 383,75 27,67 765,85 7,21% Для построенного ряда определим:
· показатели центра распределения
· показатели вариации
· показатели дифференциации и концентрации
· показатели формы распределения
По результатам расчетов сделаем вывод о характере распределения регионов по величине признака.
Показатели центра распределения:
К показателям центра распределения относятся: средняя арифметическая, мода и медиана.
Номер группы 1 2 3 4 5 6 Центр интервала, x’
205,5 248,5 272 297,3 332,7 394 Число регионов в группе, f 12 12 11 14 14 14
Средняя арифметическая —
%
Мода — наиболее часто встречающееся значение признака. Так как данный ряд имеет неравные интервалы, то модальным будет интервал с максимальной плотностью распределения.
Номер интервала (группы) 1
2
3
4
5
6
Плотность распределения, p 0,24 0,33 1,02 0,35 0,45 0,15 Длина интервала, i 49,8 36,2 10,8 39,8 31 91,6 Накопленная частота, F 12 24 34 38 52 66 Мода находится в 3 интервале (наибольшая плотность распределения, равная 1,02, соответствует именно ему). Конкретное значение моды определяется по формуле:
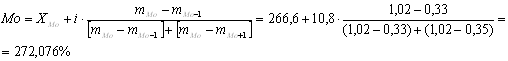
Медиана соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номеру:
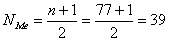
Следовательно, медианным является 5-й интервал 317,2-348,2. Численное же значение медианы определяется по формуле:
319,414%
ВЫВОД: в качестве показателя центра распределения можно выбрать любой из полученных показателей, т. к. их численные значения примерно равны.
Показатели вариации (колеблемости) признака:
Абсолютные показатели:
Размах колебаний (размах вариации):
R=Xmax-Xmin
R= 439,8-180,6 = 259,2
Для расчета показателей вариации построим дополнительную таблицу:
Группа регионов по уровню заболеваемости (на 1000 человек населения): болезни органов дыхания Число регионов, f x' x' * f d =| x' — x | d*f d2 * f
180,6 230,4 12 90,3 1083,6 205,49 2465,88 506713,68 230,4 266,6 12 115,2 1382,4 180,59 2167,08 391352,98 266,6 277,4 11 133,3 1466,3 162,49 1787,39 290433,00 277,4 317,2 14 138,7 1941,8 157,09 2199,26 345481,75 317,2 348,2 14 158,6 2220,4 137,19 1920,66 263495,35 348,2 439,8 14 174,1 2437,4 121,69 1703,66 207318,39 Итого: 77 10531,9 964,54 12243,93 2004795,14
Среднее линейное отклонение:
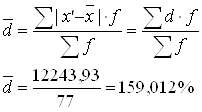
Дисперсия:

Среднее квадратичное отклонение:
%
Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем отличаются индивидуальные значения признака среднего вот его значения.
Квартильное отклонение:
Квартиль — значения признака, которые делят ранжированный ряд на четыре равные по численности части.
Сначала определим положение квартилей:
Это 2 ой интервал 230,4 — 266,6
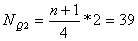
Это 3 й интервал 266,6 — 277,4
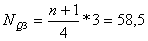
Это 4 интервал 277,4 — 317,2
Теперь найдем значение квартилей:
, где
xQ — нижняя граница интервала, в котором находится квартиль
SQ — 1 — накопленная частота интервала, предшествующего тому, в котором находится квартиль
fQ — частота интервала, в котором находится квартиль
Итак,
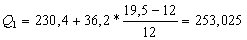
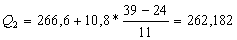
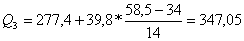
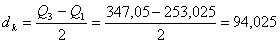
Квартильное отклонение применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений.
Относительные показатели вариации:
Коэффициент осцилляции:

Коэффициент вариации:

Вывод: совокупность данных является однородной, т. к. коэффициент вариации не превышает 33%.
Относительное линейное отклонение:

Относительный показатель квартильной вариации:

Показатели дифференциации и концентрации:
Для оценки дифференциации используем фондовый коэффициент дифференциации и коэффициент децильной дифференциации.
Фондовый коэффициент дифференциации.
8 регионов — 10% от общего числа регионов.
Среднее значение признака для 10% самых мелких единиц совокупности(180,6; 189,2; 199; 202,9; 210,1; 213,8; 215,1; 223,3; 224,4; 229,5):
208,28
Среднее значение признака для 10% самых крупных единиц совокупности(369,5; 372; 372,8; 384,4; 394,3; 396; 398,4; 399,3; 437,7; 439,8):
396,46

Коэффициент дифференциации децильной.
— номер первой децили. Она находится в 1-ом интервале 180,6 — 230,4

— номер девятой децили. Она находится в 5-ом интервале 317,2 — 348,2


Вывод: наименьший показатель признака 10% регионов с наибольшими значениями по уровню заболеваемости на 1000 человек населения: болезни органов дыхания в 5,48 раза выше наивысшего показателя уровня заболеваемости на 1000 человек населения: болезни органов дыхания 10% регионов с наименьшими значениями признака.
Для оценки концентрации единиц по значению признака используем коэффициент концентрации Джинни и коэффициент Герфендаля.
Коэффициент Джинни:


Концентрацию можно считать несущественной, т. к. 0,08<0,3
Коэффициент Герфендаля (фактический):
=
0,179
Коэффициент Герфендаля при равномерном распределении:
, где 6 — число интервалов;

Сравним фактическое значение коэффициента Герфендаля с рассчитанным значением коэффициента для равномерного распределения. Т.к. 0,179 > 0,167, то концентрация очень высокая.
Показатели формы распределения.
Относительный показатель асимметрии:

Величина показателя асимметрии положительна, следовательно асимметрия правосторонняя.
Рассчитаем показатель асимметрии вторым способом:

523514,77
2,62
Средняя квадратическая ошибка асимметрии:


Вывод: с вероятностью 99,7% асимметрия существенна (так как 9,70 > 3) и распределение признака в генеральной совокупности не является симметричным. Вследствие несимметричности распределения показатели эксцесса не рассчитываются.
