КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Статистика»


СОДЕРЖАНИЕ
ЗАДАЧА 1
					







ЗАДАЧА 2
ЗАДАЧА 3
ЗАДАЧА 4
ЗАДАЧА 5
ЗАДАЧА 6
ЗАДАЧА 7
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
ЗАДАЧА 1. Для выявления зависимости между
возрастом и числом членов семьи произвести группировку рабочих с порядковыми
номерами с 1 по 15 включительно, приведенными в таблице 1. Результаты группировки
изложить в табличной форме и сделать выводы.
Выборочные данные обследования
рабочих завода
Таблица 1

















































№ п/п
Возраст, лет
Число членов семьи


1
25
2


2
22
1


3
34
4


4
28
3


5
22
2


6
35
4


7
27
3


8
40
5


9
38
4


10
32
4


11
30
3


12
23
2


13
25
1


14
31
2


15
27
3



Решение: Произведем группировку и данные
занесем в таблицу 2.
Таблица 2



















№ п/п
Число членов семьи
Возраст, лет


1
1
22-25


2
2
22-31


3
3
27-30


4
4
32-38


5
5
40



Вывод: в возрасте от 22 до 31 года число
членов семьи колеблется от 1 до 3 человек, с увеличение возраста до 38 лет,
количество членов семьи возрастает до 4 человек, и в возрасте 40 лет – до 5
человек, т.е. с увеличением возраста увеличивается количество членов семьи.
ЗАДАЧА 2. Рассчитать абсолютные и
относительные показатели планового задания по численности рабочих и
производительности труда на основании данных, приведенных в таблице 3. 
Таблица 3










Показатели
Фактически за предыдущий год
За отчетный год


фактически
% выполнения плана



Среднесписочная численность, чел. 
Производительность труда, т/чел.


188
9,6


170
11,5


98
112




Решение:
Относительный
показатель планового задания (коэффициент планового задания) по численности рабочих:
Кпл.зад. =    =   =
0,92 · 100 – 100 = — 8 %
где, Уп – план (170 · 100 : 98 = 173)
Уо — базисный уровень, 188
Абсолютный показатель
планового задания по
численности рабочих:
188 – 173 = 15чел.
где, 188 — базисный
уровень, 173 – план.
Вывод: запланировано, по сравнению с предыдущим
годом снизить среднесписочную численность в 0,92 раза или на 8%, что
соответствует количеству 15 человек.
Относительный
показатель планового задания (коэффициент планового задания) по производительности труда
Кпл.зад. =    =   =
1,07 · 100 – 100 = 7 %
где, Уп – план (11,5 · 100 : 112 = 10,3); Уо — базисный
уровень, 9,6
Абсолютный показатель
планового задания по
производительности труда 10,3 — 9,6 = 0,7 т/чел
где, 9,6 — базисный
уровень, 10,3 – план.
Вывод: запланировано, по сравнению с
предыдущим годом, увеличить производительность труда в 1,07 раза или на 7%, что
соответствует 0,7 т/чел.
ЗАДАЧА 3. Имеются следующие данные (таблица 4)
об удельном весе продукции 1 сорта в общем выпуске по двум предприятиям:
Таблица 4










№ предприятия
Общее количество выпущенной продукции, тыс. шт.
Удельный вес продукции 1 сорта, %


1
800
55


2
745
41



Решение: рассчитаем количество продукции 1
сорта в тыс. шт. по каждому предприятию отдельно.
55 · 800 : 100 = 440
тыс.шт. продукции 1 сорта было выпущено на первом предприятии.
41 · 745 : 100 = 375
тыс.шт. продукции 1 сорта было выпущено на втором предприятии.
Всего по двум
предприятиям: 440 + 375 = 815 тыс.шт. продукции 1 сорта Общее количество выпущенной
продукции на двух предприятиях: 
800 + 745 = 1545 тыс.шт.
Рассчитаем средний
удельный вес продукции 1 сорта в общем выпуске по двум предприятиям, вместе
взятым:
Удельный вес =   · 100 =   =
53 %
Вывод: средний удельный вес продукции 1
сорта в общем выпуске по двум предприятиям составляет 53 %.
ЗАДАЧА 4. По нижеследующим данным о запасах
угля на складе шахты на 2007г., (в тыс.т) вычислить среднюю величину запаса
всеми возможными способами: 1) за каждый месяц; 2) за каждый квартал; 3) за
каждое полугодие; 4) за год.














1.01. – 15,0
1.06. – 17,3
1.11. – 14,9


1.02. – 14,8
1.07. – 17,9
1.12. – 14,5


1.03. – 15,5
1.08. – 17,5
1.01.2008г. – 14,1


1.04. – 16,2
1.09. – 16,9


1.05. – 16,8
1.10. – 15,1



Решение: найдем среднюю хронологическую
величину
Х=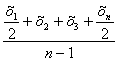  
1) Хянварь = 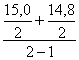 = 14,9 тыс.т.; Хфевраль
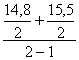=  = 15,2 тыс.т.
Хмарт =   =
15,9 тыс.т.; Хапрель =  =
16,5 тыс.т. 
Хмай =   = 17,0 тыс.т.; Хиюнь
=  = 17,6 тыс.т.
Хиюль =   =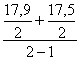
17,7 тыс.т.; Хавгуст =  =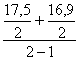
17,2 тыс.т. 
Хсентябрь =  =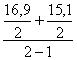
16,0 тыс.т.; Хоктябрь =   =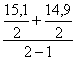
15,0 тыс.т. 
Хноябрь =  =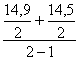
14,7 тыс.т.; Хдекабрь =   =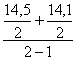
14,4 тыс.т.
2) ХI квартал = 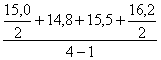  = 15,1 тыс.т.;
ХII квартал =   = 16,8 тыс.т.; 
ХIII квартал =   = 17,4 тыс.т.;
ХIV квартал =   = 14,8 тыс.т.
3) Х1
полугодие =   = 15,9 тыс.т.
Х2 полугодие =  = 16,1
4) Хгод =   = 
= 16,0 тыс.т.
ЗАДАЧА 5. Определить влияние структурных
сдвигов на изменение средней себестоимости 1 т продукции и абсолютное изменение
ее за счет структурных сдвигов по данным, приведенным в таблице 5:
Таблица 5


















№ п/п
Объем выпущенной продукции, тыс.т
Себестоимость 1 т. р.


базисный год
отчетный год
базисный год
отчетный год


1
165
125
180
165


2
385
375
65
85



Решение: 
1 предприятие
Влияние структурных
сдвигов на изменение себестоимости 1 т продукции.
Определим коэффициент
динамики по объему выпущенной продукции:
Кд =   =   =
0,76 · 100 – 100 = — 24%
где, yi – отчетный год, y1 – базисный год
Вывод: в отчетном году,
по сравнению с базисным, объем выпущенной продукции снизился в 0,76 раз или на
24 %. 
Определим коэффициент
динамики по себестоимости 1 т продукции:
Кд =   =   =
0,92 · 100 – 100 = — 8%
где, yi – отчетный год, y1 – базисный год
Вывод: в отчетном году,
по сравнению с базисным, себестоимость 1 т продукции снизилась в 0,92 раза или
на 8 %.
Абсолютное изменение
по объему выпущенной продукции.
ΔБсх = yi – y1 = 125 – 165 = — 40 тыс.т
где, yi – отчетный год, y1 – базисный год
Объем выпущенной
продукции за отчетный год снизился на 40 тыс.т. по сравнению с базисный годом
Абсолютное изменение
по средней себестоимости продукции.
ΔБсх = yi – y1 = 165 – 180 = — 15 р.
Себестоимость одной т за
отчетный год снизилась на 15 рублей по сравнению с базисный годом.
Вывод: с учетом уменьшения выпуска продукции
на 24 % (в 0,76 раз) себестоимость 1 т продукции снижается на 8 % (в 0,92 раза)
или с учетом снижения объема выпуска продукции на 40 тыс.т. себестоимость 1 т
продукции снижается на 15 рублей.
2 предприятие
Влияние структурных
сдвигов на изменение себестоимости 1 т продукции.
Определим коэффициент
динамики по объему выпущенной продукции:
Кд =   =   =
0,97 · 100 – 100 = — 3%
где, yi – отчетный год, y1 – базисный год
Вывод: в отчетном году,
по сравнению с базисным, объем выпущенной продукции снизился в 0,97 раз или на
3 %.
Определим коэффициент
динамики по себестоимости 1 т продукции:
Кд =   =   =
1,31 · 100 – 100 = 31%
где, yi – отчетный год, y1 – базисный год
Вывод: в отчетном году,
по сравнению с базисным, себестоимость 1 т продукции увеличилась в 1,31 раза
или на 31 %.
Абсолютное изменение
по объему выпущенной продукции.
ΔБсх = yi – y1 = 375 – 385 = — 10 тыс.т
где, yi – отчетный год, y1 – базисный год
Объем выпущенной
продукции за отчетный год снизился на 10 тыс.т. по сравнению с базисный годом
Абсолютное изменение
по средней себестоимости продукции.
ΔБсх = yi – y1 = 85 – 65 = 20 р.
Себестоимость одной т за
отчетный год увеличилась на 20 рублей по сравнению с базисный годом.
Вывод: с учетом снижения выпуска продукции
на 3 % (0,97 раз) себестоимость 1 т продукции увеличивается на 31 % (в 1,31
раз) или с учетом снижения объема выпуска продукции на 10 тыс.т. себестоимость
1 т продукции увеличивается на 20 рублей.
ЗАДАЧА 6. С целью изучения производительности
труда обследовано 19 % рабочих завода. В выборку попало 324 рабочих. Средние
затраты времени на обработку одной детали этими рабочими составляют 35 минут
при среднеквадратичном отклонении 7,2 минуты. С вероятностью 0,954 рассчитайте
пределы, в которых будут находиться средние затраты времени на обработку одной
детали на всем заводе.
Дано: 
N – 1705 рабочих (объем генеральной
совокупности), N = 100 · 324 : 19
= 1705
n – 324 рабочих (объем выборки, число
обследованных мест)
  в – 35 минут
τ  — 7,2 минуты
  τ — ?
Решение:
  τ – средняя генеральная;  в
– средняя выборочная
  τ =  в
± µх
µх – средняя ошибка выборки
µ =  =  = 0,4 минуты
  τ Є [  в
— µх ;  в +
µх ]
  τ Є [35 – 0,4 ; 35 + 0,4 ]
  τ Є [34,6 ; 35,4 ]
Вывод: средние затраты времени на
обработку одной детали на всем заводе находятся в пределах от 34,6 до 35,4
минут с вероятностью 0,954. 
ЗАДАЧА 7. По условию задачи № 1 (данные таблицы
2) рассчитать уравнение регрессии, характеризующее параболическую зависимость
между возрастом рабочего и числом членов его семьи. Определите тесноту связи
между указанными признаками и постройте график фактических и теоретических
значений результативного признака. 
Решение: в данной задаче возраст является
факторным (независимым) признаком, количество членов семьи результативным
(зависимым) признаком. 
Уравнение параболической
линии имеет вид:
y = ao + a1x + a2x2
где, а2
– характеризует степень ускорения или замедления кривизны параболы и при а2
> 0 парабола имеет минимум, а при а2 < 0 –
максимум;
 а1 –
характеризует крутизну кривой;
ао – вершина кривой.
Решим систему трех
нормальных уравнений
   ∑y = nao
+ a1∑x + a2∑x2
 ∑xy = ao∑x
+ a1∑x2 + a2∑x3
 ∑x2y = ao∑x2
+ a1∑x3 + a2∑х4
Для решения уравнений составим
расчетную таблицу (таблица 6)
Таблица 6
































































№ п/п
x
y
xy
x2
x3
x4
x2y
y


1
23,5
1
24
552,25
12977,875
305003,563
552,25
1,1


2
26,5
2
53
702,25
18609,625
493181,563
1404,50
2,1


3
28,5
3
86
812,25
23149,125
659778,563
2436,75
2,7


4
35
4
140
1225,00
42875,000
1500660,000
4900,00
4,2


5
40
5
200
1600,00
64000,000
2560040,000
8000,00
4,9


Итого
153,5
15
502
4891,75
161611,625
5518663,688
17293,50
15



Подставим данные таблицы в систему
нормальных уравнений:
   15 = 5ао + 153,5а1
+ 4891,75а2
 502 = 153,5ао +
4891,75а1 + 161611,625а2
 17293,50 = 4891,75ао +
161611,625а1 + 5518663,688а2
Поделим каждый член
уравнения на коэффициенты при ао и получим следующее
значение:
   3 = ао + 30,7а1 +
978,35а2
 3,27 = ао + 31,868а1
+ 1052,844а2
 3,535 = ао + 33,038а1
+ 1128,157а2
Вычтем из второго
уравнения первое, из третьего – второе:
0,270 = 1,168а1 +
74,494 а2
0,265 = 1,170а1 +
75,313 а2
Поделим каждый член уравнения на
коэффициенты при а1:
0,231 = а1 + 63,779а2
0,226 = а1 + 64,370а2
Вычтем из второго уравнения первое и
получим:
 — 0,005 = 0,591а2,
откуда а2 =   = —
0,008 
Подставим значение в уравнение:
0,231 = а1 + 63,779
( — 0,008) 
0,231 = а1 – 0,510,
откуда а1 = 0,231 + 0,510 = 0,741
Методом подстановки получаем: 
3 = ао + 30,7 ·
0,741 + 978,35 · ( — 0,008)
3 = ао + 22,749 –
7,827
3 = ао + 14,922,
откуда ао = 3 – 14,922 = — 11,922
Запишем уравнение параболы: 
y = — 11,922 + 0,741х  — 0,008х2
Определим теоретические
значения у, для чего в уравнение кривой подставим значения х
(таблица 6). 
Построим график
фактических и теоретических значений результативного признака.
  
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Годин А.М. Статистика. — Москва, 2003г. 
2. Глинский В.В. Сборник задач по общей теории статистики.-
Москва, 1999г.
3. Громыко Т.Л. Общая теория статистики. Москва. 2000г.
4. Лысенко С.Н. Общая теория статистики. Москва. 2006г.
5. Шмойлова Р.А. Теория статистики. Учебное пособие. –
Москва. 2002г.