Виды и формы индексов
Оглавление
1. Понятие
индексов, их виды
2.
Агрегатные индексы
3.
Средние индексы из индивидуальных
					







4.
Индексы среднего уровня
Цель: показать значение индексного
факторного анализа в экономических исследованиях; освоить понятия: виды
индексов, формы индексов, оказывающие влияние на сложное явление; взаимосвязь
между показателями.
После изучения вы сможете: правильно
использовать индексный метод анализа (выбирать формулу индекса; определять его
значение; выявлять влияния отдельных факторов).
Информационные источники:
1. 
Статистика: Учебник/Под ред. И.И.
Елисеевой. – М.: Крокус, 2008
2. 
Годин А.М. Статистика: Учебник. –
М.: Дашков и К’, 2008.
3. 
Теория статистики: Учебник/Под
ред. Г.П. Громыко. – М.: ИНФРА-М, 2000.
4. 
Статистика: Учебник/Под ред. В.Г.
Ионина. — М.: ИНФРА-М, 2008.
5. 
Галкина В.А. Статистика: Учебное
пособие: М.: РГАЗУ,2002.
6. 
Статистика. Учебник/Под ред. В.Г.
Ионова. — М.: ИНФРА-М, 2008.
7. 
Громыко Г.Л. Теория статистики.
Практикум. — М.: ИНФРА-М, 2008.
8. 
Теория статистики: Учебник/Под
ред. Р.А Шмойловой М.: Финансы и Статистика,2007.
Содержание темы: рассматривается
классификация индексов; приводятся формулы различных видов индексов; показан на
примере расчёт агрегатных и средних индексов.
1. Понятие индексов, их виды
Индекс (лат. — index) означает показатель, указатель, число.
По форме выражения — это относительная
величина (выражается: в коэффициентах и процентах).
Индекс — обобщенная характеристика сравнения двух совокупностей, образуемых
непосредственно несопоставимыми единицами.
Индексы сравнивают совокупности как во
времени, так и в пространстве. Методика построения индексов при этом не
меняется. Поэтому здесь индексы будут рассмотрены на примере временных сопоставлений.
По характеру изучаемых явлений индексы
подразделяются на индексы объёмных показателей (например, индексы физического,
измеренного в натуральных единицах объема производства или продажи товаров), индексы
качественных показателей (например, индексы цен, себестоимости,
производительности труда, заработной платы и пр.) и индексы сложных явлений (например,
товарооборота, затрат на производство и т.д.).
Если изучается динамика лишь одного
элемента совокупности, то строят индивидуальные индексы. Например, индекс цен
на один товар определяется по формуле
  (1.4.1)
где р0 и p1 — цены
на товар соответственно базисного и отчетного периодов.
Индивидуальные индексы по другим явлениям
строятся аналогично, но с использованием специфических обозначений.
Вот основные из них:
q — физический
объем (количество) производства или продаж;
z — себестоимость;
W —
производительность труда (выработка) работников;
l — заработная плата;
Т — численность
работников;
pq —
товарооборот (выручка от продаж) или стоимость произведенной продукции;
zq —
денежные затраты на произведенную продукцию;
IT —
фонд оплаты труда (заработной платы);
WT —
выпуск продукции.
Если изучаются не отдельные единицы
совокупности, а их группы или все без исключения единицы совокупности, то
рассчитывают групповые и общие (сводные) индексы соответственно. Их обозначение
I (index).
Общие индексы по методам построения подразделяются
на агрегатные и средние из индивидуальных. Если сравниваются не два периода
(момента), а более, то исчисляют системы цепных и базисных индексов (как
индивидуальных, так и общих). Динамика среднего уровня качественного показателя
изучается с помощью взаимосвязанных индексов переменного, постоянного составов и
структурных сдвигов.
2. Агрегатные индексы
индексный факторный агрегатный
цена
Агрегатные индексы — исходная (основная) форма общих индексов. Они
используются для изучения динамики совокупности непосредственно несопоставимых
явлений. Несопоставимость при этом преодолевается приведением элементов к
единой (стоимостной, затратной по труду и т.п.) форме путем введения в формулы
дополнительного сомножителя, соизмерителя или веса индекса. Представим основные
формулы агрегатных индексов:
1) Индекс физического объема товарооборота
(количества проданных товаров)
  (1.4.2)
2) Индекс цен на товары по методике Э. Ласперреса:
  (1.4.3)
3) Индекс цен на товары по методике Г. Пааше
  (1.4.4)
4) Индекс товарооборота (выручки от
продажи)
  (1.4.5)
Если индекс цен построен по методике Г. Пааше,
то индексы (формулы (1.4.2), (1.4.4), (1.4.5)) взаимосвязаны следующим образом:
Ipq=Ip × Iq(1.4.6)
Разность между числителем и знаменателем
соответствующих индексов показывает абсолютное изменение товарооборота pq за
счет отдельных факторов:
1) за счет изменения количества продаж
  (1.4.7)
2) за счет изменения цен
   (1.4.8)
3) за счет двух факторов вместе
   (1.4.9)
Указанные абсолютные приросты
взаимосвязаны следующим образом:
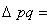
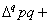
     (1.4.10)
Проиллюстрируем расчет показателей на
примере.
Пример 1.4.1. Имеются следующие данные (табл. 1.4.1).
Таблица 1.4.1 Продажи продукции на рынке
















Товар
Единица измерения
Количество продаж
Цена, руб.


в январе
в феврале
в январе
в феврале



А
Б


кг
л


1000
2000


750 .
2200


30
10


36
10





1.Определите:
1) индивидуальные индексы физического объема продаж и
цен;
2) общий индекс физического объема товарооборота;
3) общие индексы цен (по двум методикам);
4) общий индекс товарооборота;
5) абсолютные приросты выручки от продаж в целом и за
счет отдельных факторов.
2.  Покажите взаимосвязь
между исчисленными показателями.
Решение
1.1) Индивидуальные индексы определяют по
формуле (1.4.1):
для товара А
количество продаж ¾ iq =   =
0,750 , или 75,0%;
цена ¾ ip
=   = 1,2 , или 120,0%
для товара Б
количество продаж ¾ iq =   =
1,1 , или 110,0%;
цена ¾ ip
=   = 1,0 , или 100,0%
1.2) Общий индекс физического объема
определяют по формуле (1.4.2):
   , или 89,0%
Среднее по двум товарам снижение
количества продаж составило 11,0%.
1.3) Общие индексы цен вычислим по
формулам (1.4.3) и (1.4.4):
По методике Ласпейреса:
   , или 112,0%
Среднее по двум товарам повышение цен
составило 12,0%.
По методике Пааше:
   , или 110,1%
Цены на товары в среднем возросли на
10,1%.
1.4) Общий индекс товарооборота вычислим
по формуле (1.4.5):
   , или 98,0%
Выручка от продаж всех товаров сократилась
на 2,0%.
5) Абсолютные приросты товарооборота
вычислим соответственно по формулам (1.4.7), (1.4.8), (1.4.9):
в целом за счет двух факторов вместе
Δpq = 49 000 — 50 000 = — 1000 руб.;
за счет среднего изменения количества
продаж
   = 44 500-50 000
= — 5500 руб.;
за счет среднего роста цен
   = 49 000 — 44
500 = + 4500 руб.
2. Взаимосвязь индексов показывает формула
(1.4.6): 0,980 = 1,101 • 0,890.
Взаимосвязь абсолютных приростов
показывает формула (1.4.10): — 1000 = — 5500 + 4500 руб.
3. Средние индексы из индивидуальных
Часто отсутствие необходимой информации не
позволяет вычислить общие индексы в агрегатной форме. В таком случае решить
указанную проблему позволят преобразования агрегатных индексов в средние
индексы из индивидуальных.
Средний арифметический индекс физического
объема товарооборота
   (1.4.11)
где qi = iq ×q0 (исходя из того, что iq = q1
/ q0 );
средний гармонический индекс цен
   (1.4.12)
где р0
= p1 / ip (исходя
из того, что ip = p1 / p0).
Пример 1.4.2. Имеются следующие данные (табл. 1.4.2).
Таблица 1.4.2 Выпуск изделий








Изделие
Затраты на производство, тыс. руб.
Прирост (уменьшение) выпуска в отчетном периоде по
сравнению с базисным, %



А
В
С


800
600
400


 — 20
+ 10
Без изменения





Определите:
1) среднее изменение количества выпущенных изделий;
2) абсолютное изменение денежных затрат за счет среднего
изменения объема выпуска изделий;
3) среднее изменение себестоимости изделий, если
денежные затраты в целом возросли на 30%.
Решение 1. Для расчета среднего изменения количества выпущенных изделий необходимо
исчислить индекс физического объема. Его исчисляют по формуле средней
арифметической из индивидуальных индексов (1.4.11):
   , или 94,4%
Среднее снижение выпуска по всем изделиям
составило 5,6%.
2. Аналогично формуле (1.4.7) можем
записать:
  
Тогда   =
1700-1800 = — 100 тыс. руб.
3. Среднее изменение себестоимости изделий
следует исчислить, используя взаимосвязь индексов:
Izq = Iz × Iq
Откуда
Iz = Izq : Iq
где по условию задачи l.q =1,3.
Тогда
Iz =1,3 : 0,944 = 1,377 , или
137,7%.
Таким образом, среднее увеличение
себестоимости по всем изделиям составило 37,7%.
Пример 1.4.3. Торговое предприятие осуществляет продажу товаров А и
Б. Цена на товар А по сравнению с предыдущей неделей возросла в 2 раза, а на
товар Б не изменилась.
Определите среднее изменение цен, если доля товара А в выручке от продажи данной
недели составила 80%.
Решение
Преобразуем формулу (1.4.12) для замены
абсолютных значений товарооборота отчетного периода относительными (долями):
  
Подстановка исходных данных даст результат
1,667, или 166,7%. Таким образом, среднее повышение цен составило 66,7%.
4. Индексы среднего уровня
С помощью данных индексов изучается
динамика среднего уровня качественного показателя. Качественный показатель при
этом характеризует одно и то же явление (цену, себестоимость продукции,
производительность труда и т.п.), которое наблюдается на разных участках.
Средний уровень качественного признака зависит не только от самих осредняемых
величин, но и от состава (структуры) совокупности, которая определяется по объемному
признаку.
Поэтому изменение средней во времени
зависит от изменения собственно значений признака и от изменения структуры
совокупности.
Методику расчета индексов среднего уровня
покажем на примере индексов себестоимости переменного, постоянного составов и
структурных сдвигов.
Индекс себестоимости переменного состава /f
(средней себестоимости) вычисляется по формуле
   (1.4.13)
При этом абсолютное изменение средней
себестоимости Δz определяется разницей между   и
  данного индекса:
   (1.4.14)
   и   показывают
относительное и абсолютное изменение средней себестоимости за счет двух
факторов — среднего изменения собственно себестоимостей и изменения структуры
выпуска продукции.
Индекс себестоимости постоянного состава  , характеризующий изменение
средней себестоимости за счет только себестоимости, рассчитывают по формуле
   (1.4.15)
Абсолютное изменение средней себестоимости
за счет изменения только себестоимости отдельных видов продукции рассчитываются
по формуле
   (1.4.16)
Индекс структурных сдвигов Iстр
показывает относительное изменение средней себестоимости за счет изменения
структуры выпуска продукции на отдельных участках и определяется по формуле
   (1.4.17)
При этом абсолютное изменение средней
себестоимости за счет указанного фактора вычисляется по формуле
   (1.4.18)
Вычисленные по указанным методикам
показатели взаимосвязаны, а именно:
      ×   (1.4.19)
абсолютные приросты
      ×   (8.20)
Пример 1.4.4. Имеются следующие данные (табл. 1.4.3).
Таблица 1.4.3 Производство продукта А














Предприятие
Себестоимость, руб.
Выпуск, шт.


в базисном периоде
в отчетном периоде
в базисном периоде
в отчетном периоде



1
2


50
80


60
90


500
1000


1000
1000





Определите:
1) индексы себестоимости переменного, постоянного
составов и структурных сдвигов;
2) абсолютные приросты средней себестоимости по двум
факторам вместе и по каждому фактору в отдельности.
Покажите взаимосвязь между показателями. Сделайте выводы.
Решение
1) Индекс себестоимости переменного
состава (формула 1.4.13)
   , или 107,1%
индекс себестоимости постоянного состава (формула
1.4.15):
   , или 115,4%
индекс структурных сдвигов (формула
1.4.17):
  = 65:70 = 0,928 , или 92,8%.
2) Абсолютный прирост средней
себестоимости за счет двух факторов (формула 1.4.14):  75-70 = 5 руб.;
абсолютный прирост средней себестоимости
за счет среднего роста собственно себестоимости (формула 1.4.16):  75-65 = 10 руб.;
абсолютный прирост за счет изменения
структуры выпуска продукта (формула 1.4.18):  65-70
= — 5руб.
Взаимосвязь между индексами отражает формула (1.4.19): 1,071 = 1,154 0,928;
между абсолютными приростами — формула
(1.4.20): 5 = 10-5 руб.
Выводы. Средняя себестоимость продукта А возросла
на 7,1%, или на 5 руб., за счет двух факторов:
а) за счет снижения себестоимости по
предприятиям средняя себестоимость возросла на 15,4%, или на 10 руб.;
б) за счет изменения структуры выпуска
продукта (структурного сдвига), т.е. увеличения доли выпуска   на предприятии 1 с 33,3%   до 50%   , где себестоимость ниже.
Структурный сдвиг, т.е. увеличение доли
выпуска продукта на предприятии с низким уровнем себестоимости (предприятие 1,
где себестоимость в базисном периоде составляла 50 руб.) привело к снижению
средней себестоимости на 7,2%, или на 5 руб.