Храм знаний Эвенкия

Анализ данных в линейной регрессионной модели
Дата: 21.05.2016 

		
Государственное образовательное учреждение высшего профессионального
образования


«Московский государственный институт электронной технки


(технический универститет)»


Курсовая работа


по дисциплине

					










«Теория вероятности и математическая статистика»


Тема работы


«Анализ данных в линейной регрессионной модели»


Выполнил:


Студент
группы ЭКТ — 21


Рыжов
С.А.         


Проверил:


Преподаватель


Бардушкина
И. В.


Москва — 2010


Вариант
20.


Задание
1


Выполнить
предварительную обработку результатов наблюдений, включающую:


1 
построение
диаграммы рассеивания (корреляционного поля);


2 
группировку
данных и построение корреляционной таблицы;


3 
оценку числовых
характеристик для негруппированных и группированных данных.


Оценка числовых
характеристик для негруппированных данных:





















































































































































































































































X
Y
X
Y




4,19
9,19
4,44
9,13




3,04
11,94
11,31
4,58




4,6
8,09
7,57
3,14




9,83
10,33
1,62
14,61




8,66
7,15
5,71
6,48




1,3
12,34
11,06
6,78




4,22
16,35
10,35
2,15




5,11
7,7
2,46
9,66




9,85
5,64
1,02
11,19




8,8
4,52
5,77
7,77




12,17
4,52
8,63
4,05




11,25
2,06
6,91
4,76




5,73
7,41
3,56
8,54




4,05
10,51
9,47
2,22




5,41
9,97
6,16
3,72




1,28
14,68
8,26
3,57




1,67
9,67
6,7
14,32




11,99
3,31
4,95
10,64




7,66
5,93
3,37
10,73




5,17
9,87
1,53
10,13




3,26
11,52
9,54
4,95




12,58
2,88
3,11
5,38




8,34
3,57
5,09
5,79




5,79
4,39
11,08
3,87




3,42
9,71
8,74
 — 2,23




Сумма X
317.78




Сумма Y
369,18






MX


6,3556






MY


7,3836






s2X


11,02005






s2Y


15,31479






KXY


 — 9,1594






ρXY


 — 0,7194









Числовые характеристики
для негруппированной выборки находятся по следующим формулам:


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


Построение
корреляционного поля:


 Анализ данных в линейной регрессионной модели 


Построение корреляционной
таблицы:


Таблица 1.1



















































































































Y


X


 — 1.5
1.5
4.5
7.5
10.5
13.5
16.5


ni.






2.5
0
0
1
1
8
3
0
13




5.5
0
0
4
5
6
1
1
17




8.5
1
1
8
1
1
0
0
12




11.5
0
3
4
1
0
0
0
8






nj.


1
4
17
8
15
4
1
50









Оценка числовых характеристик
для группированных данных:


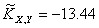
 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ,        Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ,   Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели  = — 0.87


Задание 2


Для негруппированных
данных проверить гипотезу Анализ данных в линейной регрессионной модели  об отсуствии линейной статистической
связи между компонентами X и Y при альтернативной гипотезе Анализ данных в линейной регрессионной модели ( уровень значимости α = 0,05);


Выборочное значение
статистики равно 


 Анализ данных в линейной регрессионной модели ,


 Анализ данных в линейной регрессионной модели 


Используя средства Matlab, найдем


 Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели 


Так как выборочное
значение статистики больше квантили распределения Стьюдента, гипотеза H0 отклоняется в сторону гипотезы H1. Корреляция значима. 


Задание 3


Для негруппированых
данных получить интервальную оценку для истинного значения коэффициента
корреляции ρX,Y, при уровне значимости α = 0,05.


Используя средства Matlab, найдем


 Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели ,     Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели ,     Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели 


Задание 4


Для негруппированных и
группированных данных составить уравнения регрессии Y на x и X на Y.


Рассмотрим вначале случай
негруппированных данных. 


 Анализ данных в линейной регрессионной модели 


Этот интервал не содержит
нуля, т.е. с доверительной вероятностью 1 – ЫВА = 0,95 существует корреляция
между X и Y и имеет смысл построение уравнений регрессии.


 Анализ данных в линейной регрессионной модели ,  Анализ данных в линейной регрессионной модели 


y(x) = 12,77 – 0,848*x;


x(y) = 10,86 – 0,6*y;


Проверка.


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели .


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели 


Случай группированных
данных.


Подставим найденные
значения Анализ данных в линейной регрессионной модели  в
уравнеиня линейной регрессии Y
на x и X на y. Получим:


y(x) = 17,14 – 1,4*x;


x(y) = 10,83 – 0,54*y;


Проверка: Анализ данных в линейной регрессионной модели 


Задание 5


Для негруппированных
данных нанести графики выборочных регрессионных прямых на диаграмму
рассеивания. 


 Анализ данных в линейной регрессионной модели 


Задание 6


Для негруппированных
данных по найденным оценкам параметров линейной регрессии Y на x получить оценку s2 для дисперсии ошибок наблюдений σ2, найти коэффициент детерминации R2, построить доверительные интервалы
для параметров регрессии a и b, дисперсии ошибок наблюдений σ2 и среднего значения Y при x = x0 .


Для негруппированных
данных были получены следующие оценки числовых характеристик и коэффициентов
регрессии: Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели .


Используя соотношение Анализ данных в линейной регрессионной модели , вычислим
остаточную сумму  Анализ данных в линейной регрессионной модели 


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели .


 Анализ данных в линейной регрессионной модели ;


Тогда оценка дисперсии
ошибок наблюдений равна


 Анализ данных в линейной регрессионной модели .


Коэффициент детерминации
равен


 Анализ данных в линейной регрессионной модели .


Поскольку Анализ данных в линейной регрессионной модели (знак Анализ данных в линейной регрессионной модели ) Анализ данных в линейной регрессионной модели , то сделаем проверку
правильности расчетов:


 Анализ данных в линейной регрессионной модели (верно).


Полученный результат для
коэффициента детерминации означает, что уравнение регрессии Анализ данных в линейной регрессионной модели  на 49,7% объясняет
общий разброс результатов наблюдений относительно горизонтальной прямой Анализ данных в линейной регрессионной модели .


Построим доверительные
интервалы для параметров линейной регрессии и дисперсии ошибок наблюдений.


С помощью Matlab найдем квантили распределений
Стьюдента и Анализ данных в линейной регрессионной модели :


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели ;


– доверительный интервал
для параметра Анализ данных в линейной регрессионной модели :






 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


– доверительный интервал
для параметра Анализ данных в линейной регрессионной модели :


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели ;


– доверительный интервал
для дисперсии ошибок наблюдений Анализ данных в линейной регрессионной модели :


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели .


-Найдем границы
доверительных интервалов для среднего значения Анализ данных в линейной регрессионной модели  при Анализ данных в линейной регрессионной модели :


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели .


Задание 7. Для негруппированных данных
проверить значимость линейной регрессии Y на x
(уровень значимости α
= 0,05). 


Гипотеза Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели  отклоняется на уровне
значимости Анализ данных в линейной регрессионной модели ,
так как доверительный интервал  Анализ данных в линейной регрессионной модели  не накрывает нуль с
доверительной вероятностью 0,95.


Этот же результат можно
получить, используя для проверки гипотезу Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели  и статистику Анализ данных в линейной регрессионной модели .


С помощью Matlab найдем квантили распределения
Фишера:


 Анализ данных в линейной регрессионной модели ,                   Анализ данных в линейной регрессионной модели .


Выборочное значение
статистики Анализ данных в линейной регрессионной модели  равно:


 Анализ данных в линейной регрессионной модели .


Поскольку Анализ данных в линейной регрессионной модели Анализ данных в линейной регрессионной модели , то гипотеза Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели  отклоняется на уровне
значимости Анализ данных в линейной регрессионной модели .
Таким образом, линейная регрессия Анализ данных в линейной регрессионной модели  на Анализ данных в линейной регрессионной модели  статистически значима.


Задание №8


Для данных,
сгруппированных только по Анализ данных в линейной регрессионной модели , проверить адекватность линейной
регрессии Анализ данных в линейной регрессионной модели  на
Анализ данных в линейной регрессионной модели  (уровень
значимости Анализ данных в линейной регрессионной модели ).


Для проверки адекватности
воспользуемся корреляционной таблицей. Будем считать, что середины интервалов
группировки Анализ данных в линейной регрессионной модели ,
Анализ данных в линейной регрессионной модели , являются
значениями компоненты Анализ данных в линейной регрессионной модели . Тогда число Анализ данных в линейной регрессионной модели  повторных наблюдений
равно 4. Запишем результаты этих наблюдений в виде таблицы 






Таблица 1.2















































 Анализ данных в линейной регрессионной модели 


2,5
5,5
8,5
11,5






 Анализ данных в линейной регрессионной модели 




11,94


12,34


14,68


9,87


11,52


9,71


14,61


9,66


11,19


8,54


10,73


10,13


5,38




9,19


8,09


16,35


7,70


7,41


10,51


9,97


9,87


4,39


6,48


7,77


4,76


3,72


14,32


10,64


5,79


9,13




10,33


7,15


5,64


4,52


4,52


3,57


3,14


4,05


2,22


3,57


4,95


 — 2,23




4,52


2,06


3,11


2,88


4,58


6,78


2,15


3,87








 Анализ данных в линейной регрессионной модели 


13
17
12
8






 Анализ данных в линейной регрессионной модели 


10,79
8,59
9,65
3,74









Для удобства расчетов в
последней строке таблицы приведены средние значения Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели .


 Анализ данных в линейной регрессионной модели .


Получим уравнение
выборочной линейной регрессии Анализ данных в линейной регрессионной модели  на Анализ данных в линейной регрессионной модели  для данных, сгруппированных по Анализ данных в линейной регрессионной модели :


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели ;


y(x) = 8,29 – 0,9x.


 Анализ данных в линейной регрессионной модели ;


 Анализ данных в линейной регрессионной модели .


Выборочное значение
статистики Анализ данных в линейной регрессионной модели  равно


 Анализ данных в линейной регрессионной модели .


Так как квантиль
распределения Фишера, вычисленный с помощью Matlab, равен


 Анализ данных в линейной регрессионной модели 3,19,


то Анализ данных в линейной регрессионной модели , а значит, линейная
регрессия Анализ данных в линейной регрессионной модели  на
Анализ данных в линейной регрессионной модели  для
данных, сгруппированных по Анализ данных в линейной регрессионной модели , адекватна результатам
наблюдений.


Задание 9. Для негруппированных данных проверить
гипотезу Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели при
альтернативной гипотезе Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели (уровень значимости Анализ данных в линейной регрессионной модели )


Имеются следующие
величины: Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели , , Анализ данных в линейной регрессионной модели , Анализ данных в линейной регрессионной модели .


Сначала проверяется
гипотеза Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели ,
альтернативная гипотеза Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели .


Статистика равна


 Анализ данных в линейной регрессионной модели  = 1,931


С помощью средств Matlab, найдем:


F0,975 (n — 1; n — 1)=F0,975 (49,49) = 1.7622


z > F0,975 (n — 1;
n — 1), 


следовательно Анализ данных в линейной регрессионной модели отклоняется, а
значит что Анализ данных в линейной регрессионной модели 


Теперь можно проверить
гипотезу, Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели , при
альтернативной гипотезе Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели .


Т.к. Анализ данных в линейной регрессионной модели , статистика имеет вид


 Анализ данных в линейной регрессионной модели  = 1,418


Найдем количество степеней
свободы


 Анализ данных в линейной регрессионной модели ≈3,625


С помощью средств Matlab, найдем:


 Анализ данных в линейной регрессионной модели 


z < Анализ данных в линейной регрессионной модели , значит нет оснований отклонять
гипотезу Анализ данных в линейной регрессионной модели : Анализ данных в линейной регрессионной модели .






Приложение


A = [
4.19 3.04 4.60 9.83 8.66 1.30 4.22 5.11 9.85 8.80 12.17 11.25 5.73 4.05 5.41
1.28 1.67 11.99 7.66 5.17 3.26 12.58 8.34 5.79 3.42 4.44 11.31 7.57 1.62 5.71
11.06 10.35 2.46 1.02 5.77 8.63 6.91 3.56 9.47 6.16 8.26 6.70 4.95 3.37 1.53
9.54 3.11 5.09 11.08 8.74; 


 9.19 11.94 8.09
10.33 7.15 12.34 16.35 7.70 5.64 4.52 4.52 2.06 7.41 10.51 9.97 14.68 9.67 3.31
5.93 9.87 11.52 2.88 3.57 4.39 9.71 9.13 4.58 3.14 14.61 6.48 6.78 2.15 9.66
11.19 7.77 4.05 4.76 8.54 2.22 3.72 3.57 14.32 10.64 10.73 10.13 4.95 5.38 5.79
3.87 — 2.23]


 x =
A(1,:);


 y =
A(2,:);


 Mx = mean(x)


 Dx = var(x,1)


 My = mean(y)


 Dy = var(y,1)


 plot(x,y,«g*»)


 grid on


 hold on


 axis([1 13 — 3 18]);


 gca1 = gca;


 set(gca1,«xtick»,[1 4 7 10 13],«ytick»,[ — 3 0 3 6 9 12 15 18]);


 xlabel(«X»);


 ylabel(«Y»);


 z =
12.77 — 0.848*x; %построение регрессии Y на x


 Zplot = plot(z,x);


 set(Zplot,«Color»,«Red»,«LineWidth»,[2])


 hold on


 text(12, — 1,«x(y)»); 


 text(11.8,
2,«y(x)»);


 t =
10.86 — 0.6*y; %построение регрессии X на y


 Tplot = plot(t,y);


 set(Tplot,«Color»,«Red»,«LineWidth»,[2])


 hp =
line([1 6.36],[7.38 7.38]); %эти прямые показывают положение 


 set(hp,«Color»,«blue»,«LineWidth»,[1.5])
%среднего выборочного


 hp = line([6.36 6.36],[ — 3
7.38]);


 set(hp,«Color»,«blue»,«LineWidth»,[1.5])


 K =
cov(x,y) %находим ковариацию


 DEtK
= det(K)


 M =
corrcoef(x,y) %коэффициент корреляции


 detM
= det(M)

Метки:
Автор: 

Опубликовать комментарий