Содержание

Введение
Глава
1. Общие понятия проверки статистических гипотез
1.1
Сущность и виды проверки статистических гипотез
1.2
Выбор критериев для проверки статистических гипотез
					







1.3
Основные принципы расчета критериев для проверки статистических гипотез
Глава
2. Проверка различных типов статистических гипотез 
2.1
Проверка гипотезы о законе распределения генеральной совокупности с
использованием критерия Пирсона
2.2
Проверка гипотезы с неизвестной дисперсией генеральной совокупности согласно
критерию Стьюдента
2.3.
Проверка гипотезы о законе распределения генеральной совокупности с
использованием функции Лапласа
2.4
Проверка гипотезы о законе распределения генеральной совокупности с
использованием критерия Фишера-Снедекора
Заключение
Список
литературы
Приложение
1
Приложение
2
Приложение
3
Приложение
4
Введение
Актуальность.
Последние
годы отмечены стремительным расширением области применения
теоретико-вероятностных и статистических методов. Они применяются в различных
науках: физике, техники, геологии, биологии, лингвистике, медицине, социологии,
управлении и т. д. Один из основных разделов статистики — теория проверки
статистических гипотез. Понятие практической статистики, процедура
обоснованного сопоставления высказанной гипотезы относительно природы или
величины неизвестных статистических параметров анализируемого явления с
имеющимися в распоряжении исследователя выборочными данными (выборкой).
Статистическая
проверка гипотез проводится с помощью некоторого статистического критерия по
общей логической схеме, включающей нахождение конкретного вида функции от
результатов наблюдения (критической статистики), на основании которой
принимается окончательное решение. Например, могут рассматриваться гипотезы об
общем законе распределения исследуемой случайной величины, об однородности двух
или нескольких обрабатываемых выборок, о числовых значениях параметров
исследуемой генеральной совокупности и др. Результат проверки может быть либо
отрицательным (данные наблюдения противоречат высказанной гипотезе), либо
неотрицательным. В первом случае гипотеза ошибочна, во втором – ее нельзя
считать доказанной: просто она не противоречит имеющимся выборочным данным,
однако таким же свойством могут наряду с ней обладать и другие гипотезы. Для
статистической проверки гипотез используются разные критерии. В частности,
когда проверяется согласие между выборочным и гипотетическим распределениями,
используется критерий согласия, например, критерий Пирсона «хи-квадрат»,
критерий Колмогорова-Смирнова и др.
Статистические
критерии приводятся вместе с указанием как тех областей, где их применение
вполне оправдано, так и тех областей, где применение требует осторожности.
Большое внимание уделено построению критериев, в том или ином смысле наилучших. 
Цель
работы: ознакомиться с процессом проверки статистических
гипотез. 
Поставленная
цель определила задачи работы:
1.
Определить сущность, понятие проверки статистических гипотез.
2.
Рассмотреть этапы проверки статистических гипотез.
3.
Рассмотреть критерии проверки статистических гипотез.
4.
Ознакомиться с различными проверками статистических гипотез.
Структура
работы: данная работа состоит из введения, двух глав,
заключения, списка литературы и приложения. Во введении изложен ход предстоящей
работы. 1 глава содержит теоретическое описание общих понятий проверки
статистических гипотез. Во 2 главе приведены расчеты проверок различных типов
статистических гипотез. В заключении подведены итоги работы, сделаны выводы.
Список литературы включает литературные источники, используемые в ходе работы.
В приложении представлен материал, необходимый для проверки статистических
гипотез.
Глава
1. Общие понятия проверки статистических гипотез
1.1
Сущность и виды проверки статистических гипотез
В
процессе статистического анализа иногда бывает необходимо сформулировать и
проверить предположения (гипотезы) относительно величины независимых параметров
или закона распределения изучаемой генеральной совокупности (совокупностей). 
Например,
исследователь выдвигает гипотезу о том, что «выборка извлечена из нормальной
генеральной совокупности» или «генеральные средние двух анализируемых совокупностей
равны». Такие предположения называются статистическими гипотезами.
Сопоставление
высказанной гипотезы относительно генеральной совокупности с имеющимися выборочными
данными, сопровождаемое количественной оценкой степени достоверности
получаемого вывода и осуществляемое с помощью того или иного статистического
критерия, называется проверкой статистических гипотез.
Под
статистической гипотезой понимаются различного рода предположения относительно
характера или параметров распределения случайной переменной, которые можно
проверить, опираясь на результаты наблюдений в случайной выборке.
Иными
словами, статистической гипотезой называется предположение о свойстве
генеральной совокупности, которое можно проверить, опираясь на данные выборки.
Обозначается гипотеза буквой Н. Так, может быть выдвинута гипотеза о
том, что средняя в генеральной совокупности равна некоторой величине.
Смысл
проверки статистической гипотезы состоит в том, чтобы по имеющимся
статистическим данным принять или отклонить статистическую гипотезу с
минимальным рисков ошибки. Эта проверка осуществляется по определенным
правилам.
Следует
иметь в виду, что статистическая проверка гипотез имеет вероятностный характер.
С помощью статистической проверки гипотез можно определить вероятность принятия
ложного решения по тем или иным результатам статистического изучения данного
явления. Если вероятность ошибки невелика, то статистические показатели исчисленные
при изучении явления, могут быть использованы для практических целей при малом
риске ошибки.
Гипотезы
в свою очередь классифицируются на:
—
простые и сложные;
—
параметрические и непараметрические;
—
основные (высказанные) и альтернативные (конкурирующие).
Если
выдвигаемая гипотеза сводится к утверждению о том, что значение некоторого
неизвестного параметра генеральной совокупности в точности равно заданной
величине, то эта гипотеза называется простой. 
Например:
«Среднедушевой совокупный доход населения России составляет 10000 рублей в
месяц»; «Уровень безработицы (доля безработных в численности экономически
активного населения) в России равен 9%».
Сложной
называют гипотезу, которая состоит из конечного или бесконечного множества
простых гипотез, при этом указывается некоторая область вероятных значений
параметра.
Гипотезы
о параметрах генеральной совокупности называются параметрическими, о
распределениях — непараметрическими.
Выдвинутая
гипотеза называется нулевой (основной). Ее принято обозначать Н0.
При этом предполагается, что действительное различие сравниваемых величин равно
нулю, а выявленное по данным отличие от нуля носит случайный характер. Нулевая
гипотеза отвергается тогда, когда по выборке получается результат, который при
истинности выдвинутой нулевой гипотезы маловероятен. 
По
отношению к высказанной (основной) гипотезе всегда можно сформулировать
альтернативную (конкурирующую), противоречащую ей. Альтернативную
(конкурирующую) гипотезу принято обозначать Н1.
В
качестве нулевой гипотезы Н0 принято выдвигать простую гипотезу, так
как обычно бывает удобнее проверять более строгое утверждение.
По
своему содержанию статистические гипотезы можно подразделить на несколько
основных типов:
—
гипотезы о виде закона распределения исследуемой случайной величины;
—
гипотезы о числовых значениях параметров исследуемой генеральной совокупности;
—
гипотезы об однородности двух или нескольких выборок или некоторых
характеристик анализируемых совокупностей;
—
гипотезы об общем виде модели, описывающей статистическую зависимость между
признаками; и др.
Так
как проверка статистических гипотез осуществляется на основании выборочных
данных, т.е. ограниченного ряда наблюдений, решения относительно нулевой
гипотезы Н0 имеют вероятностный характер. Другими словами, такое
решение неизбежно сопровождается некоторой, хотя возможно и очень малой,
вероятностью ошибочного заключения как в ту, так и в другую сторону.
Так,
в какой-то небольшой доле случаев а нулевая гипотеза Н0 может
оказаться отвергнутой, в то время как в действительности в генеральной
совокупности она является справедливой. Такую ошибку называют ошибкой 1-го
рода, а ее вероятность – уровнем значимости и обозначают.
Наоборот,
в какой-то небольшой доле случаев (нулевая гипотеза Н0
принимается, в то время как на самом деле в генеральной совокупности она ошибочна,
а справедлива альтернативная гипотеза Нх. Такую ошибку
называют ошибкой 2-го рода. Вероятность ошибки 2-го рода обозначается как Вероятность
1 — называют мощностью критерия.
При
фиксированном объеме выборки можно выбрать по своему усмотрению величину
вероятности только одной из ошибок. Увеличение вероятности одной из них
приводит к снижению другой. 
Принято
задавать вероятность ошибки 1-го рода  уровень значимости. Как
правило, пользуются некоторыми стандартными значениями уровня значимости: 0,1;
0,05; 0,025; 0,01; 0,005; 0,001. Тогда, очевидно, из двух критериев,
характеризующихся одной и той же вероятностью а (отклонить правильную в действительности
гипотезу Н0), следует принять тот, которому соответствует
меньшая ошибка 2-го рода, т.е. большая мощность. Снижения вероятностей обеих
ошибок и можно добиться путем увеличения объема выборки.
Правильное
решение относительно нулевой гипотезы Н0 также может быть
двух видов:
—
будет принята нулевая гипотеза Н0, когда в генеральной
совокупности верна нулевая гипотеза Н0; вероятность такого
решения 1;
—
нулевая гипотеза Н0 будет отклонена в пользу альтернативной Н1,
когда в генеральной совокупности нулевая гипотеза Н0 отклоняется
в пользу альтернативной Н1; вероятность такого решения 1 мощность
критерия.
Результаты
решения относительно нулевой гипотезы можно проиллюстрировать с помощью таблицы
1.
статистический гипотеза проверка лаплас
Таблица
1












Нулевая
гипотеза Н0

Результаты
решения относительнонулевой гипотезы Н0


Отклонена
Принята


Верна

Ошибка
1-го рода,
ее
вероятность
Р(Н1/
Н0) = 


Правильное
решение,
его
вероятность
Р(Н0/
Н0) = 1 — 



Неверна

Правильное
решение,
его
вероятность
Р(Н1/
Н1) = 1-


Ошибка
2-го рода, ее
вероятность
Р((Н0/
Н0)= 




В
отношении свойств генеральной совокупности могут выдвигаться некоторые гипотезы
о величине средней, дисперсии, характере распределения, форме и тесноте связи между
переменными. 
Проверка
гипотезы осуществляется на основе выявления согласованности эмпирических данных
с гипотетическими (теоретическими). Если расхождение между сравниваемыми
величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом
не делается никаких заключений о правильности самой гипотезы, речь идет лишь о
согласованности сравниваемых данных. 
Основой
проверки статистических гипотез являются данные случайных выборок, При этом
безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической
генеральной совокупности. Последнее открывает путь применения этого метода за
пределами собственно выборки: при анализе результатов эксперимента, данных
сплошного наблюдения, но малой численности. В этом случае рекомендуется
проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств,
насколько она характерна для того комплекса условий, в которых находится
изучаемая совокупность.
Особенно
часто процедура проверки статистических гипотез проводится для оценки существенности
расхождений сводных характеристик отдельных совокупностей (групп): средних, относительных
величин. Такого рода задачи, как правило, возникают в социальной статистике.
Трудоемкость статистико-социологических исследований приводит к тому, что почти
все они строятся на несплошном учете. Поэтому проблема доказательности выводов
в социальной статистике стоит особенно остро. Применяя процедуру проверки
статистических гипотез, следует помнить, что она может гарантировать результаты
с определенной вероятностью лишь по «беспристрастным» выборкам, на основе
объективных данных.
1.2.
Выбор критериев для проверки статистических гипотез
Проверка
статистических гипотез осуществляется с помощью статистического критерия
(назовем его в общем виде К), являющегося функцией от результатов
наблюдения.
Статистический
критерий – это правило (формула), по которому определяется мера расхождения
результатов выборочного наблюдения с высказанной гипотезой Н0.
Как
уже отмечалось выше, следует иметь в виду, что статистическая проверка гипотез
имеет вероятностный характер, так как принимаемые вывод основываются на изучении
свойств распределения случайной переменной по данным выборки, а потому всегда
существует риск допустить ошибку. Однако с помощью статистической проверки
гипотез можно определить вероятность принятия ложного решения. Если вероятность
последнего невелика, то можно считать, что применяемый критерий обеспечивает
малый риск ошибки.
При
проведении проверки статистических гипотез в первую очередь приходится решать
задачи статистической проверки гипотез о:
1)
принадлежности «выделяющихся» единиц исследуемой выборочной совокупности
генеральной совокупности;
2)
виде распределения изучаемых признаков;
3)
величине средней арифметической и доли;
4)
наличии и тесноте связи между изучаемыми признаками;
5)
о форме корреляционной связи.
При
проверке гипотез имеется возможность совершить ошибку двоякого рода:
а)
ошибка первого рода — проверяемая гипотеза (нулевая гипотеза Н0)
является в действительности верной, но результаты проверки приводят к отказу от
нее; 
б)
ошибка второго рода — проверяемая гипотеза в действительности является
ошибочной, но результаты проверки приводят к принятию.
В
статистике в настоящее время имеется большое число критериев для проверки
практически любых гипотез. Притом основные принципы их построения и применения
являются общими. Для построения статистического критерия, позволяющего
проверить некоторую гипотезу, необходимо следующее:
1)
сформулировать проверяемую гипотезу Н0. Наряду с проверяемой
гипотезой формулируется также конкурирующая (альтернативная) гипотеза;
2)
выбрать уровень значимости, контролирующий допустимую вероятность ошибки
первого рода; 
3)
определить область допустимых значений и так называемую критическую область;
4)
принять то или иное решение на основе сравнения фактического и критического
значений критерия.
Проверка
статистических гипотез складывается из следующих этапов:
—
формулируется в виде статистической гипотезы задача исследования;
—
выбирается статистическая характеристика гипотезы;
—
выбираются испытуемая и альтернативная гипотезы на основе анализа возможных
ошибочных решений и их последствий;
—
определяются область допустимых значений, критическая область, а также
критическое значение статистического критерия (t,
F) по соответствующей таблице;
—
вычисляется фактическое значение статистического критерия;
—
проверяется испытуемая гипотеза на основе сравнения фактического и критического
значений критерия, и в зависимости от результатов проверки гипотеза либо
отклоняется, либо не отклоняется.
Уровнем
значимости будет называться такое малое значение вероятности попадания критерия
в критическую область при условии справедливости гипотезы, что появление этого
события может расцениваться как следствие существенного расхождения выдвинутой
гипотезы и результатов выборки. Обычно уровень значимости принимают равным 0,05
или 0,01. Исходя из величины уровня значимости, можно определить критическую
область, под которой понимается такая область значений выборочной характеристики,
попадая в которую они будут свидетельствовать о том, что проверяемая гипотеза
должна быть отвергнута. К критической области относятся те значения, появление
которых при условии верности гипотезы было бы маловероятным.
Допустим,
что рассчитанное по эмпирическим данным значение критерия попало в критическую
область, тогда при условии верности проверяемой гипотезы Н0 вероятность
этого события будет не больше уровня значимости. Поскольку выбирается достаточно
малым, то такое событие является маловероятным и, следовательно, проверяемая
гипотеза Н0 может быть отвергнута.
Если
же наблюдаемое значение характеристики не принадлежит к критической области и, следовательно,
находится в области допустимых значений, то проверяемая гипотеза Н0
не отвергается. Вероятность попадания критерия в область допустимых значений
при справедливости проверяемой гипотезы Н0 равна 1.
Чем
меньше уровень значимости, тем меньше вероятность браковать проверяемую
гипотезу, когда она верна, т.е. меньше вероятность совершить ошибку первого
рода. Но при этом расширяется область допустимых значений и, значит,
увеличивается вероятность совершения ошибки второго рода.
Все
значения рассматриваемой характеристики, не принадлежащие к критической области
образуют так называемую область допустимых значений. Если наблюдаемое значение
характеристики находится в области допустимых значений, то проверяемая гипотеза
принимается с вероятностью.
Выбор
критерия для проверки статистических гипотез может осуществляться на основании
различных принципов. Чаще всего для этого пользуются принципом отношения
правдоподобия, который позволяет построить критерий, наиболее мощный среди всех
возможных критериев. Суть его сводится к выбору такого критерия К с
известной функцией плотности f(k)
при
условии справедливости гипотезы Н0, чтобы при заданном
условии значимости можно было бы найти критическую точку Ккр
распределения f(k),
которая
распределила бы область допустимых значений, в которой результаты выборочного
наблюдения выглядят наиболее правдоподобными, и критическую область, в которой
результаты выборочного наблюдения выглядят менее правдоподобными в отношении
нулевой гипотезы Н0.
Если
такой критерий К выбран, и известна плотность его распределения, то
задача проверки статистической гипотезы сводится к тому, чтобы при заданном
уровне значимости рассчитать по выборочным данным наблюдаемое значение
критерия Кнабл и определить, является ли оно наиболее или
наименее правдоподобным в отношении нулевой гипотезы Н0.
Проверка
каждого типа статистических гипотез осуществляется с помощью соответствующего
критерия, являющегося наиболее мощным в каждом конкретном случае.
Как
уже отмечалось ранее, проверка статистических гипотез применяется в разных
областях для изучения массовых явлений. Изучение массовых явлений, как правило,
осуществляется по неполной информации. В составе собранных данных могут
встречаться единичные наблюдения, у которых отдельные значения изучаемых
признаков заметно отличаются от общей тенденции изменения большинства значений.
Причины таких отличий могут быть разными:
1)
из-за ошибок наблюдения; 
2)
вследствие случайного стечения различных обстоятельств, каждый из которых в
отдельности несущественный, но совокупное их влияние привело к таким резко
выделяющимся от общей картины значениям признаков; 
3)
как следствие нарушения однородности изучаемой совокупности. 
В
общем случае все значения изучаемых признаков фиксируются по известным единицам
совокупности по их части, отобранной с учетом всех требований. Следовательно,
первичные статистические данные, включая и резко «выделяющемся», соответствуют
конкретным случаям проявления изучаемого явления. Следовательно,
субъективное отбрасывание «выделяющихся» единиц недопустимо.
Рассмотрим
использование критериев для проверки статистических гипотез на примере закона
нормального распределения. Закон нормального распределения лежит в основе
многих теорем и методов статистики 
—
при оценке репрезентативности выборки (расчете ошибки выборки и распространении
характеристик выборки на генеральную совокупность);
—
измерении степени тесноты связи и составлении модели регрессии;
—
построении и использование статистических критериев и др.
Как
показывают многочисленные статистические исследования, частоты (частости)
эмпирических распределений за редким исключением будут отличаться от значений
теоретического распределения. Расхождения между частотами (частостями)
эмпирического и теоретического распределения могут быть несущественными и
объяснены случайностями выборки и существенными при несоответствии выбранного и
эмпирического законов распределения.
Для
проверки гипотезы о соответствии эмпирического распределения теоретическому
закону нормального распределения используются особые статистические
показатели-критерии согласия (или критерии соответствия). К ним относятся
критерии К.Пирсона, А.Н. Колмогорова,
Романовского, Ястремского и др.
Большинство
критериев согласия базируется на использовании отклонений эмпирических частот
от теоретических. Очевидно, что чем больше эти отклонения, тем хуже
теоретическое распределение соответствует эмпирическому. Статистические
характеристики таких критериев согласия являются некоторыми функциями этих
отклонений.
1.3.
Основные принципы расчета критериев для проверки статистических гипотез
Проверка
каждого типа статистических гипотез осуществляется с помощью соответствующего
критерия, являющегося наиболее мощным для в каждом конкретном случае. Например,
проверка гипотезы о виде закона распределения случайной величины может быть
осуществлена с помощью критерия согласия Пирсона 2; проверка
гипотезы о равенстве неизвестных значений дисперсий двух генеральных
совокупностей — с помощью критерия Фишера F;
ряд гипотез о неизвестных значениях параметров генеральных совокупностей
проверяется с помощью критерия Z
—
нормальной распределенной случайной величины и критерия t-Стьюдента
и т. д.
Значение
критерия, рассчитываемое по специальным правилам на основании выборочных данных,
называется наблюдаемым значением критерия (Кнабл.).
Значения
критерия, разделяющие совокупность значений критерия на область допустимых
значений (наиболее правдоподобных в отношении нулевой гипотезы Н0)
и критическую область (область значений, менее правдоподобных в отношении
нулевой гипотезы Н0), определяемые на заданном уровне
значимости а по таблицам распределения случайной величины К, выбранной в
качестве критерия, называются критическими точками (Ккр).
Областью
допустимых значений (областью принятия нулевой гипотезы Н0)
называют совокупность значений критерия К, при которых нулевая гипотеза Н0
не отклоняется.
Критической
областью называют совокупность значений критерия К, при которых нулевая
гипотеза Н0 отклоняется в пользу конкурирующей Н1.
Различают
одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
Если
конкурирующая гипотеза — правосторонняя, например, Н1: а >
а0, то и критическая область правосторонняя (рисунок 1). При
правосторонней конкурирующей гипотезе критическая точка (К кр.п)
принимает положительные значения.
  
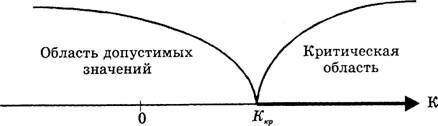
Рисунок
1
Если
конкурирующая гипотеза — левосторонняя, например, Н1: а <
а0, то и критическая область — левосторонняя (рисунок 2). При
левосторонней конкурирующей гипотезе критическая точка принимает отрицательные
значения (Ккр.л).
  
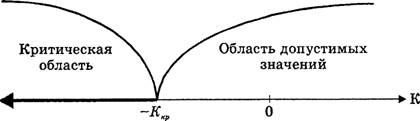
Рисунок
2.
Если
конкурирующая гипотеза — двусторонняя, например, Н1: а=а0,
то и критическая область — двусторонняя (рисунок 3). При двусторонней
конкурирующей гипотезе определяются 2 критические точки (Ккр.л и Ккр.п).
  
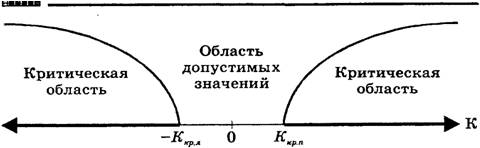
Рисунок
3
Основной
принцип проверки статистических гипотез состоит в следующем:
—
если наблюдаемое значение критерия (Кнабл) принадлежит критической
области, то нулевая гипотеза Н0 отклоняется в пользу
конкурирующей;
—
если наблюдаемое значение критерия (Кнабл) принадлежит области
допустимых значений, то нулевую гипотезу Н0 нельзя отклонить.
Можно
принять решение относительно нулевой гипотезы Н0 путем
сравнения наблюдаемого (Кнабл) и критического значений критерия (Ккр).
При
правосторонней конкурирующей гипотезе:
—
если Кнабл < Ккр, то нулевую гипотезу Н0
нельзя отклонить;
—
если Кнабл > Ккр, то нулевая гипотеза Н0 отклоняется
в пользу конкурирующей Н1.
При
левосторонней конкурирующей гипотезе:
—
если Кнабл >— Ккр, то нулевую гипотезу Н0
нельзя отклонить;
—
если Кнабл < — Ккр, то нулевая гипотеза Н0
отклоняется в пользу конкурирующей Н1.
При
двусторонней конкурирующей гипотезе:
—
если — Ккр < Кнабл < Ккр, то
нулевую гипотезу Н0 нельзя отклонить;
—
если Кнабл > Ккр или Кнабл < -Ккр, то
нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1.
Алгоритм
проверки статистических гипотез сводится к следующему:
 1)
сформулировать нулевую Н0 и альтернативную Н1
гипотезы;
2)
выбрать уровень значимости ;
3)
в соответствии с видом выдвигаемой нулевой гипотезы Н0 выбрать
статистический критерий для ее проверки, т.е. — специально подобранную случайную
величину К точное или приближенное распределение которой заранее
известно;
4)
по таблицам распределения случайной величины К, выбранной в качестве
статистического критерия, найти критическое значение К (критическую точку или
точки);
5)
на основании выборочных данных по специальному алгоритму вычислить наблюдаемое
значение критерия Кнабл;
6)
по виду конкурирующей гипотезы Н1 определить тип критической
области;
7)
определить, в какую область (допустимых значений или критическую) попадает
наблюдаемое значение критерия Кнабл, и в зависимости от этого -принять
решение относительно нулевой гипотезы Н0.
Следует
заметить, что даже в том случае, если нулевую гипотезу Н0 нельзя
отклонить, это не означает, что высказанное предположение о генеральной
совокупности является единственно подходящим: просто ему не противоречат
имеющиеся выборочные данные, однако таким же свойством наряду с высказанной
могут обладать и другие гипотезы.
Можно
интерпретировать результаты проверки нулевой гипотезы следующим образом:
—
если в результате проверки нулевую гипотезу Н0 нельзя
отклонить, то это означает, что имеющиеся выборочные данные не позволяют с
достаточной уверенностью отклонить нулевую гипотезу Н0,
вероятность нулевой гипотезы Н0 больше, а конкурирующей Н1
– меньше 1 — ;
—
если в результате проверки нулевая гипотеза Н0 отклоняется в
пользу конкурирующей Н1, то имеющиеся выборочные данные не
позволяют с достаточной уверенностью принять нулевую гипотезу Н0,
вероятность нулевой гипотезы Н0 меньше, а конкурирующей Н1
– больше 1 -.
Глава
2. Проверка различных типов статистических гипотез
2.1
Проверка гипотезы о законе распределения генеральной совокупности с использованием
критерия Пирсона
Использование
этого критерия основано на применении такой меры (статистики) расхождения между
теоретическим F(x) и эмпирическим распределением Fn(x),
которая приближенно подчиняется закону распределения. Гипотеза Н0
о согласованности распределений проверяется путем анализа распределения этой
статистики. Применение критерия требует построения статистического ряда.
(Приложение 1).
Пример
1. В 7 случаях из 10 фирма-конкурент компании «А» действовала на рынке так, как
будто ей заранее были известны решения, принимаемые фирмой «А». На уровне значимости
0,05 определите, случайно ли это, или в фирме «А» работает осведомитель
фирмы-конкурента?
Решение.
Для того чтобы ответить на поставленный вопрос, необходимо проверить
статистическую гипотезу о том, совпадает ли данное эмпирическое распределение
числа действий фирмы-конкурента с равномерным теоретическим распределением?
Если
ходы, предпринимаемые конкурентом, выбираются случайно, т. е. в фирме «А» – нет
осведомителя (инсайдера), то число «правильных» и «неправильных» ее действий
должно распределиться поровну, т. е. по 5 (10/2), а это и есть отличительная
особенность равномерного распределения.
Этот
вид статистических гипотез относится к гипотезам о виде закона распределения
генеральной совокупности.
Сформулируем
нулевую и конкурирующую гипотезы согласно условию задачи.
Н0:
X ~ R(а;
b) – случайная величина X
подчиняется равномерному распределению с параметрами (а; b)
(в контексте задачи – «В фирме «А» –нет осведомителя (инсайдера)»;
«Распределение числа удачных ходов фирмы-конкурента – случайно»);
Н1:
случайная величина X не подчиняется равномерному распределению (в
контексте задачи – «В» фирме «А» – есть осведомитель (инсайдер)»; «Распределение
числа удачных ходов фирмы-конкурента – неслучайно»).
В
качестве критерия для проверки статистических гипотез о неизвестном законе распределения
генеральной совокупности используется случайная величина %2. Этот критерий
называют критерием Пирсона.
Его
наблюдаемое значение (2набл)
рассчитывается по формуле
   
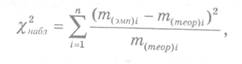
где
m(эмп) i
–
эмпирическая частота i-й
группы выборки; m(теор)
i
–
теоретическая частота i
-й
группы выборки.
Составим
таблицу распределения эмпирических и теоретических частот (таблица 2).
Таблица
2









m(эмп)
i

7
3



m(теор)
i

5
5




Найдем
наблюдаемое значение 2набл
  
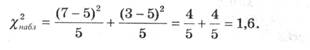
Критическое
значение (2кр) следует определять с помощью таблиц
распределения 2 по уровню значимости и числу степеней свободы k.
По
условию = 0,05, а число степеней свободы рассчитывается по формуле
k =
n – l
– 1
где
k —
число степеней свободы; n
–
число групп выборки; l
–
число неизвестных параметров предполагаемой модели, оцениваемых по данным
выборки (если все параметры предполагаемого закона известны точно, то l
=
0).
По
условию задачи, число групп выборки (n)
равно 2, так как могут быть только 2 варианта действий фирмы-конкурента:
«удачные» и «неудачные», а число неизвестных параметров равномерного
распределения (l) равно 0.
Отсюда
k =
2- 0-1 = 1.
Найдем
2кр по уровню значимости а = 0,05 и числу степеней
свободы k
=
1:
2кр(a=0,05; k =1)=3,8
2набл
< 2кр, следовательно, на данном уровне значимости
нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических
частот — незначимые. Данные наблюдений согласуются с гипотезой о равномерном
распределении генеральной совокупности.
Это
означает, что для утверждения о том, что действия фирмы-конкурента на рынке
неслучайны, нет оснований и на уровне значимости = 0,05 можно утверждать, что в
фирме «А» нет платного осведомителя фирмы-конкурента.
Ответ.
На уровне значимости = 0,05 можно утверждать, что в фирме «А» нет платного
осведомителя фирмы-конкурента.
Пример
2. На уровне значимости = 0,025 проверить гипотезу о нормальном распределении
генеральной совокупности, если известны эмпирические и теоретические частоты
(табл. 3):
Таблица
3

















m(эмп)
i

5
10
20
25
14
3



m(теор)
i

6
14
28
18
8
3




Решение.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0:
X ~ N(2)
— случайная величина X подчиняется нормальному закону распределения с
параметрами и 2.
Н1:
случайная величина X не подчиняется нормальному закону распределения с
параметрами и 2.
В
качестве критерия для проверки нулевой гипотезы используем критерий Пирсона 2.
Найдем
наблюдаемое значение (2набл ):
  
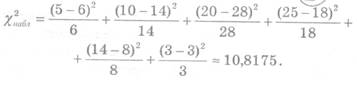
Найдем
критическое значение критерия (2кр) по таблице
распределения 2кр по уровню значимости и числу степеней
свободы k.
По
условию = 0,025; число степеней свободы найдем по формуле
k =
n – l
– 1
где
k –
число степеней свободы; n
—
число групп выборки; l
–число
неизвестных параметров предполагаемой модели, оцениваемых по данным выборки.
По
условию задачи число групп выборки (n)
равно 6, а число неизвестных параметров нормального распределения (l)
равно 2.
Отсюда
k = 6- 2-1 = 3.
Найдем
2кр по уровню значимости = 0,025 и числу степеней свободы
k = 3:
2кр
(=0,025; k =3) = 9,4
2
набл > 2кр, следовательно, на данном уровне
значимости нулевая гипотеза отклоняется в пользу конкурирующей, расхождения
эмпирических и теоретических частот – значимые. Данные наблюдений не
согласуются с гипотезой о нормальном распределении генеральной совокупности.
Ответ.
На уровне значимости = 0,025 данные наблюдений не согласуются с гипотезой о
нормальном распределении генеральной совокупности.
2.2
Проверка гипотезы с неизвестной дисперсией генеральной совокупности согласно
критерию Стьюдента 
Цель
использования критерия Стьюдента — выявление достоверности различия между данными
двух выборок одной и той же генеральной совокупности
Метод
Стьюдента применяется для сравнения двух выборок, взятых из одной и той же
генеральной совокупности, или двух различных состояний одной и той же
выборочной совокупности. 
При
этом могут представиться следующие случаи: 
1.
По объему:
а)
обе группы большие (n>30); 
б)
обе группы малые  ;
в)
одна — большая, вторая — малая. 
2.
По составу: 
а)
группы с попарно-зависимыми вариантами, когда i- варианта первой группы
сравнивается с i- вариантой второй группы  ;
б)
группы с попарно-независимыми вариантами (можно менять варианты местами внутри
группы).
Пример.
Техническая норма предусматривает в среднем 40 с на выполнение определенной
технологической операции на конвейере по производству часов. От работающих на
этой операции поступили жалобы, что они в действительности затрачивают на нее
больше времени. Для проверки данной жалобы произведены хронометрические
измерения времени выполнения этой технологической операции у 16 работниц,
занятых на ней, и получено среднее время выполнения операции X = 42 с.
Можно ли по имеющимся хронометрическим данным на уровне значимости = 0,01
отклонить гипотезу о том, что среднее время выполнения этой операции
соответствует норме, если: 
а)
исправленное выборочное среднее квадратическое отклонение s
– 3,5 с; 
б)
выборочное среднее квадратическое отклонение 3,5 с?
Решение,
а) Для решения данной задачи необходимо проверить гипотезу о том, что
неизвестная генеральная средняя нормальной совокупности точно равна
определенному числу, когда дисперсия генеральной совокупности неизвестна
(выборка мала, так как n
= 16 меньше 30).
Сформулируем
нулевую и конкурирующую гипотезы согласно условию задачи.
Н0:
а = а0 = 40 – неизвестное математическое ожидание а (нормально
распределенной генеральной совокупности с неизвестной дисперсией) равно гипотетически
предполагаемому числовому значению а0 (применительно к условию
данной задачи — время выполнения технологической операции соответствует норме).
Н1:
а > 40 – неизвестное математическое ожидание а (нормально распределенной
генеральной совокупности с неизвестной дисперсией) больше числового значения а0
(применительно к условию данной задачи – время выполнения технологической
операции больше установленной нормы).
Так
как конкурирующая гипотеза – правосторонняя, то и критическая область –
правосторонняя.
В
качестве критерия для сравнения неизвестного математического ожидания а
(нормально распределенной генеральной совокупности с неизвестной дисперсией) с
гипотетическим числовым значением а0 используется случайная величина
t-критерий Стьюдента.
(Приложение 2).
Его
наблюдаемое значение (t
набл)
рассчитывается по формуле
  
где
X – выборочная средняя; а0 – числовое значение генеральной
средней; s
–
исправленное среднее квадратическое отклонение; n
– объем выборки.
Найдем
наблюдаемое значение t
набл
  
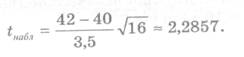
Критическое
значение (tкр)
следует находить с помощью таблиц распределения Стьюдента (приложение 2) по
уровню значимости и числу степеней свободы k.
По
условию = 0,01; число степеней свободы найдем по формуле
k = n
— 1,
где
k —
число степеней свободы; n
—
объем выборки.
k = 16 — 1 = 15.
Найдем
tкр
по уровню значимости = 0,01 (для односторонней критической области) и числу
степеней свободы k = 15:
tкр(
k
=15)=
2,6
Заметим,
что при левосторонней конкурирующей гипотезе Н1:а < 40tкр
следует находить по таблицам распределения Стьюдента (приложение 2) по уровню
значимости (для односторонней критической области) и числу степеней свободы k
= n – 1 и присваивать ему знак
«минус».
При
двусторонней конкурирующей гипотезе Н1: а≠40t следует
находить по таблицам распределения Стьюдента (приложение 2) по уровню
значимости а (для двусторонней критической области) и числу степеней свободы k
= n – 1.
t набл
< tкр следовательно,
на данном уровне значимости нет оснований отклонить нулевую гипотезу.
Ответ.
По имеющимся хронометрическим данным на уровне значимости а = 0,01 нельзя
отклонить гипотезу о том, что среднее время выполнения этой операции
соответствует норме. Следовательно, жалобы работниц — необоснованны.
Наблюдаемое
значение критерия попадает в область допустимых значений (рисунок 4),
следовательно, нет оснований отклонить нулевую гипотезу.
  
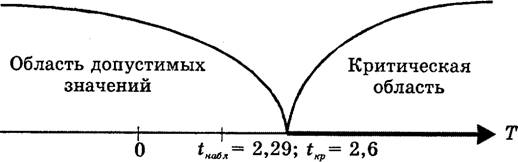
Рисунок
4
б)
Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная
генеральная средняя нормальной совокупности точно равна определенному числу,
когда дисперсия генеральной совокупности неизвестна.
Алгоритм
решения задачи будет тот же, что и в первом случае. Однако наблюдаемое значение
t набл
рассчитывается
по формуле
  
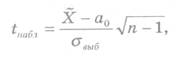
где
X — выборочная средняя; а0 — числовое значение генеральной средней; выб
— выборочное среднее квадратическое отклонение; n
—
объем выборки.
Найдем
наблюдаемое значение (t
набл)
  
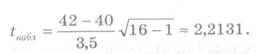
Критическое
значение (tкр)
следует находить находить по таблице распределения Стьюдента (приложение 2) по уровню
значимости а и числу степеней свободы k.
t набл
< t
кр,
следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу,
жалобы работниц — необоснованны.
Ответ.
По имеющимся хронометрическим данным на уровне значимости а = 0,01 нельзя
отклонить гипотезу о том, что среднее время выполнения этой операции
соответствует норме, жалобы работниц — необоснованны.
2.3
Проверка гипотезы о законе распределения генеральной совокупности с
использованием функции Лапласа
Пример.
Экономический анализ труда предприятий отрасли позволил выдвинуто гипотезу о
наличии 2 типов предприятий с различной средней величиной показателя производительности
труда. Выборочное обследование 42 предприятий 1-й группы дало следующие
результаты: средняя производительность труда X – 119 деталей. По данным
выборочного обследования, на 35 предприятиях 2-й группы средняя
производительность труда Y
– 107 деталей. Генеральные дисперсии известны: D(Х)
= 126,91 (дет.2); D(Y)
= 136,1 (дет.2).
Считая,
что выборки извлечены из нормально распределенных генеральных совокупностей X и
Y, на уровне значимости 0,05,
проверьте, случайно ли полученное различие средних показателей
производительности труда в группах или же имеются 2 типа предприятий с
различной средней величиной производительности труда.
Решение.
Для решения данной задачи необходимо сравнить 2 средние нормально
распределенных генеральных совокупностей, генеральные дисперсии которых
известны (большие независимые выборки). В данной задаче речь идет о больших
выборках, так как nх
= 42 и nу
= 35 больше 30. Выборки – независимые, так как из контекста задачи видно, что
они извлечены из непересекающихся генеральных совокупностей.
Сформулируем
нулевую и конкурирующую гипотезы согласно условию задачи.
Н0:
X = Y – генеральные
средние 2 нормально распределенных совокупностей с известными дисперсиями равны
(применительно к условию данной задачи – предприятия 2 групп относятся к
одному типу предприятий: средняя производительность труда в 2 группах –
одинакова).
Н1:
X≠ Y- генеральные
средние 2 нормально распределенных совокупностей с известными дисперсиями
неравны (применительно к условию данной задачи — предприятия 2 групп относятся
к разному типу предприятий: средняя производительность труда в 2 группах –
неодинакова).
Выдвигаем
двустороннюю конкурирующую гипотезу, так как из условия задачи не следует, что необходимо
выяснить больше или меньше производительность труда в одной из групп
предприятий по сравнению с другой.
Поскольку
конкурирующая гипотеза – двусторонняя, то и критическая область –
двусторонняя.
В
качестве критерия для сравнения 2 средних генеральных совокупностей, дисперсии
которых известны (большие независимые выборки), используется случайная величина
Z.
Его
наблюдаемое значение (Zнабл)
рассчитывается по формуле
  
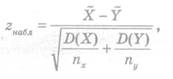
где
X – выборочная средняя для X; Y
–
выборочная средняя для Y;
1>(Х) – генеральная дисперсия для X; D(Y)
– генеральная дисперсия для Y;
пх – объем выборки для X; пу – объем выборки для Y.
Найдем
наблюдаемое значение (zнабл):
  
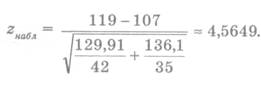
Так
как конкурирующая гипотеза — двусторонняя, критическое значение (zкр)
следует находить по таблице функции Лапласа (приложение 3) из равенства
Ф(zкр)=
(1)
По
условию = 0,05.
Отсюда
Ф0(zкр)=(1-0,05)
/2 = 0,475.
По
таблице функции Лапласа (приложение 3) найдем, при каком (zкр)
Ф0(zкр)=0,475.
Ф0(1,96)
= 0,475.
Учитывая,
что конкурирующая гипотеза — двусторонняя, находим две критические точки:
zкр(n)
= 1,96; zкр(л) =
— 1,96
Заметим,
что при левосторонней конкурирующей гипотезе Н1: X < Yzкр
следует находить по таблице функции Лапласа (приложение 3) из равенства Ф0(zкр)
= (1 — 2)/2 и присваивать ему знак «минус».
При
правосторонней конкурирующей гипотезе Н1: X > Yzкр
находим по таблице функции Лапласа (приложение 3) из равенства Ф0(zкр)
= (1 — 2)/2.
Zнабл
> zкр,
следовательно, на данном уровне значимости нулевая гипотеза отвергается в
пользу конкурирующей. На уровне значимости = 0,05 можно утверждать, что
полученное различие средних показателей производительности труда в группах неслучайно,
имеются 2 типа предприятий с различной средней величиной производительности труда.
Наблюдаемое
значение критерия попадает в критическую область (рисунок 5), следовательно,
нулевая гипотеза отклоняется в пользу конкурирующей.
  
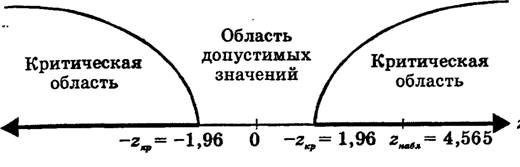
Рисунок
5
Ответ.
На уровне значимости = 0,05 можно утверждать, что полученное различие средних
показателей производительности труда в группах неслучайно, имеются 2 типа
предприятий с различной средней величиной производительности труда.
2.4
Проверка гипотезы о законе распределения генеральной совокупности с
использованием критерия Фишера-Снедекора
Пример.
Предполагается, что применение нового типа резца сократит время обработки
некоторой детали. Хронометраж времени обработки 9 деталей, обработанных старым
типом резцов, дал следующие результаты: среднее время обработки детали X – 57
мин, исправленная выборочная дисперсия s2х
= 186,2 (мин2). Среднее время обработки 15 деталей, обработанных
новым типом резцов, — Y
по данным хронометражных измерений — 52 мин, а исправленная выборочная
дисперсия s2х
= 166,4 (мин2). На уровне значимости = 0,01 ответьте на вопрос,
позволило ли использование нового типа резцов сократить время обработки детали?
Решение.
Для решения данной задачи необходимо сравнить 2 средние нормально
распределенных генеральных совокупностей, генеральные дисперсии которых
неизвестны, но предполагаются одинаковыми (малые независимые выборки). В этой
задаче речь идет о малых выборках, так как nх
= 9 и nу
= 15 меньше 30. Выборки — независимые, поскольку из контекста задачи видно, что
они извлечены из непересекающихся генеральных совокупностей.
Сформулируем
нулевую и конкурирующую гипотезы согласно условию задачи.
Н0:X
= Y —
генеральные средние 2 нормально распределенных совокупностей с неизвестными
дисперсиями (но предполагаемыми одинаковыми) равны (применительно к условию
данной задачи -среднее время, затрачиваемое на обработку детали резцами нового
и старого типа, — одинаково, т. е. использование нового типа резца не позволяет
снизить время на обработку детали).
Н1:
X > Y
—
генеральная средняя для X больше, чем генеральная средняя для Y
(применительно к условию данной задачи — среднее время, затрачиваемое на
обработку детали резцами старого типа, больше, чем — нового, т. е.
использование нового типа резца позволяет снизить время на обработку детали).
Так
как конкурирующая гипотеза — правосторонняя, то и критическая область —
правосторонняя.
Приступать
к проверке гипотезы о равенстве генеральных средних 2 нормально – распределенных
совокупностей с неизвестными дисперсиями можно лишь в том случае, если
генеральные дисперсии равны. В противном случае, данная задача в теории
неразрешима.
Поэтому,
прежде чем проверять эту гипотезу, проверим гипотезу о равенстве генеральных дисперсий
нормальных совокупностей.
Сформулируем
нулевую и конкурирующую гипотезы, согласно условию задачи.
Н0:
D(Х)=D(Y)
— генеральные дисперсии 2 нормально распределенных совокупностей равны.
Н0:
D(Х) >D(Y)
— генеральная дисперсия для X больше генеральной дисперсии для У. Выдвигаем
правостороннюю конкурирующую гипотезу, так как исправленная выборочная
дисперсия для X значительно больше, чем исправленная выборочная дисперсия для Y.
Так
как конкурирующая гипотеза — правосторонняя, то и критическая область — правосторонняя.
В
качестве критерия для сравнения 2 дисперсий нормальных генеральных
совокупностей используется случайная величина Р — критерий Фишера-Снедекора
(приложение 4).
Его
наблюдаемое значение (fнабл)
рассчитывается по формуле
  
где
s —
большая (по величине) исправленная выборочная дисперсия; s2
— меньшая (по величине) исправленная выборочная дисперсия.
Найдем
fнабл
  
Критическое
значение (fкр)
следует находить с помощью таблицы распределения Фишера-Снедекора (приложение
4) по уровню значимости и числу степеней свободы k
и k2.
По
условию а = 0,01; число степеней свободы найдем по формуле
k1
= n1 —
1; k
2
= n2
— 1,
где
k1
— число степеней свободы большей (по величине) исправленной дисперсии; k
2
— число степеней свободы меньшей (по величине) исправленной дисперсии; n1
— объем выборки большей (по величине) исправленной дисперсии; n2—
объем выборки меньшей (по величине) исправленной дисперсии.
Найдем
k1
и k
2
k1
= 10 — 1 = 9;
k 2
= 15 — 1 = 14.
Определяем
fкр
по уровню значимости = 0,01 и числу степеней свободы k1=9
и k
2
=14:
fкр( = 0,01; k1=9;
k
2 =14)
fнабл<
fкр
следовательно, на данном уровне значимости нет оснований отвергнуть нулевую
гипотезу о равенстве генеральных дисперсий нормальных совокупностей.
Следовательно,
Можно приступить к проверке гипотезы о равенстве генеральных средних двух
нормально распределенных совокупностей.
Найдем
tнабл
  
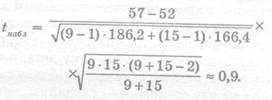
Критическое
значение (tкр)
следует находить по таблице распределения Стьюдента (приложение 2) по уровню
значимости и числу степеней свободы k.
По
условию = 0,01; число степеней свободы найдем по формуле
k = nх
+ ny — 2,
г
де
k —
число степеней свободы; nх
— объем выборки для X; ny
—
объем выборки для Y.
k = 9 + 15 — 2 = 22.
Найдем
tкр
по уровню значимости = 0,01 (для односторонней критической области) и числу
степеней свободы k = 22
Заметим,
что при левосторонней конкурирующей гипотезе X < Y
tкр
следует находить по таблицам распределения Стьюдента (приложение 2) по уровню
значимости (для односторонней критической области) и числу степеней свободы k
= nх
+ ny – 2 и присваивать ему
знак «минус». 
При
двусторонней конкурирующей гипотезе Х≠Y
tкр находим
по таблицам распределения Стьюдента (приложение 3) по уровню значимости (для
двусторонней критической области) и числу степеней свободы k
= nх
+ ny – 2.
tнабл
< tкр
следовательно, на этом уровне значимости нет оснований отвергнуть нулевую
гипотезу.
По
имеющимся хронометрическим данным на уровне значимости а = 0,01 нельзя
отклонить гипотезу о том, что генеральные средние равны, т. е. среднее время,
затрачиваемое на обработку детали старым и новым типом резцов, отличается
незначимо, расхождения между средними — случайны, использование нового типа
резцов не позволяет снизить время обработки детали.
Наблюдаемое
значение критерия попадает в область допустимых значений (рисунок 6),
следовательно, нулевую гипотезу нельзя отклонить.
  
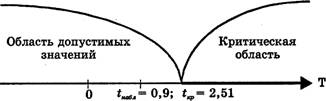
Рисунок
6
Ответ.
На уровне значимости = 0,01 нельзя утверждать, что использование нового типа
резцов позволило сократить время обработки детали.


Заключение
Проверка
статистических гипотез – необходимая методика, используемая для получения
данных в статистике. 
Проведенная
работа позволила сделать следующие выводы:
—
Под статистической гипотезой понимаются различного рода предположения
относительно характера или параметров распределения случайной переменной,
которые можно проверить, опираясь на результаты наблюдений в случайной выборке.
—
Смысл проверки статистической гипотезы состоит в том, чтобы по имеющимся
статистическим данным принять или отклонить статистическую гипотезу с
минимальным рисков ошибки. Эта проверка осуществляется по определенным
правилам.
—
Гипотезы классифицируются на: простые и сложные; параметрические и
непараметрические; основные (высказанные) и альтернативные (конкурирующие).
—
Проверка гипотезы осуществляется на основе выявления согласованности эмпирических
данных с гипотетическими (теоретическими).
—
Особенно часто процедура проверки статистических гипотез проводится для оценки
существенности расхождений сводных характеристик отдельных совокупностей
(групп): средних, относительных величин. Такого рода задачи, как правило, возникают
в социальной статистике.
—
Проверка статистических гипотез осуществляется с помощью статистического
критерия (назовем его в общем виде К), являющегося функцией от
результатов наблюдения.
—
В статистике в настоящее время имеется большое число критериев для проверки
практически любых гипотез. 
—
Выбор критерия для проверки статистических гипотез может осуществляться на
основании различных принципов. Чаще всего для этого пользуются принципом
отношения правдоподобия, который позволяет построить критерий, наиболее мощный
среди всех возможных критериев.
—
Для каждой проверки статистических гипотез существует определенный алгоритм.
Список
литературы
1. 
Аллен
Р. Статистика. – М., 2005.
2. 
Богородская,
Н.А. Статистика финансов. — М., 2005.
3. 
Виноградова
Н.М. Общая теория статистики. – М., 2000.
4. 
Гинзбург
А.И. Статистика. – СПб., 2003.
5. 
Голуб
Л.А. Социально-экономческая статистика – М., 2001.
6. 
Гусаров
В.М. Теория статистики. – М., 2008.
7. 
Джессен
Л.Статистические методы. – СПб., 2001.
8. 
Елисеева
И.И,. Юзбашев М.М Общая теория статистики. — М., 1995.
9. 
Елисеева
И.И. Обработка статистических данных. – М., 2001.
10. 
Ефимова
М.Р., Петрова Е.В., Румянцева В.Н. Общая теория статистики. — М., 1996.
11. 
Курс
социально-экономической статистики / Под ред. М.Г. Назарова. – Киев, 2005.
12. 
Льюис
К.Д. Методы прогнозирования статистических данных. – М., 2009.
13. 
Милс
Ф. Статистические методы. – М., 1996.
14. 
Ниворожкина
Л.И. Основы статистики. — М., 2000.
15. 
Общая
теория статистики [Текст]: учебник / Под ред. П.Р. Куликова. — М., 2002.
16. 
Переяслова
И.Г. Основы статистики. – Ростов н/Д, 2007.
17. 
Практикум
по социально-экономической статистике/ Под ред..М.Южина. – СПб., 2001.
18. 
Рябушкин
Т.В. Финансы и статистика. – М., 2002.
19. 
Салин
В.М. Социально-экономическая статистика. – М., 2004.
20. 
Сиденко,
А.В. Статистика. — М., 2000.
21. 
Статистика
Л.П. Харченко, В.Г. Долженкова, В.Г. Ионин [и др.]; под ред. В.Г. Ионина. – М.,
2001.
22. 
Статистика
/ Под ред. И.И. Егорова, С.В. Курышева. — М., 2005.
23. 
Статистика
финансов /Под ред. М.В. Вахрамеева, — М., 2003.
24. 
Шабалин
О.П. Социально-экономическая статистика. – М., 2003.
25. 
Четыркин
Е.М. Статистические методы прогнозирования. – М., 2005.
26. 
Экономическая
статистика / Под ред. Ю.Н. Иванова. – Мн., 1996.
27. 
Яковлев
С.В. Статистика. – М., 2005.
Приложение
1
Таблица
критерия Пирсона




























































































































































































































Число
степеней
свободы
k

Уровень
значимости


0,01
0,025
0,05
0,95
0,975
0,99


1
6,6
5,0
3,8
0,0039
0,00098
0,00016


2
9,2
7,4
6,0
0,103
0,051
0,020


3
11,3
9,4
7,8
0,352
0,216
0,115


4
13,3
ПД
9,5
0,711
0,484
0,297


5
15,1
12,8
ПД
1,15
0,831
0,554


6
16,8
14,4
12,6
1,64
1,24
0,872


7
18,5
16,0
14,1
2,17
1,69
1,24


8
20,1
17,5
15,5
2,73
2,18
1,65


9
21,7
19,0
16,9
3,33
2,70
2,09


10
23,2
20,5
18,3
3,94
3,25
2,56


11
24,7
21,9
19,7
4,57
3,82
3,05


12
26,2
23,3
21,0
5,23
4,40
3,57


13
27,7
24,7
22,4
5,89
5,01
4,11


14
29,1
26,1
23,7
6,57
5,63
4,66


15
30,6
27,5
25,0
7,26
6,26
5,23


16
32,0
28,8
26,3
7,96
6,91
5,81


17
33,4
30,2
27,6
8,67
7,56
6,41


18
34,8
31,5
28,9
9,39
8,23
7,01


19
36,2
32,9
30,1
10,1
8,91
7,63


20
37,6
34,2
31,4
10,9
9,59
8,26


21
38,9
35,5
32,7
11,6
10,3
8,90


22
40,3
36,8
33,9
12,3
11,0
9,54


23
41,6
38,1
35,2
13,1
11,7
10,2


24
43,0
39,4
36,4
13,8
12,4
10,9


25
44,3
40,6
37,7
14,6
13,1
11,5


26
45,6
41,9
38,9
15,4
13,8
12,2


27
47,0
43,2
40,1
16,2
14,6
12,9


28
48,3
44,5
41,3
16,9
15,3
13,6


29
49,6
45,7
42,6
17,7
16,0
14,3


30
50,9
47,0
43,8
18,5
16,8
15,0




Приложение
2
Критические
точки распределения Стьюдента

















































































































































































































































Число
степеней
свободы
k


Уровень
значимости 
(двусторонняя
критическая значимость)



0,10
0,05
0,02
0,01
0,002
0,001


1
6,31
12,7
31,82
63,7
318,3
637,0


2
2,92
4,30
6,97
9,92
22,33
31,6


3
2,35
3,18
4,54
5,84
10,22
12,9


4
2ДЗ
2,78
3,75
4,00
7,17
8,61


5
2,01
2,57
3,37
4,03
5,89
6,86


6
1,94
2,45
3,14
3,71
5,21
5,96


7
1,89
2,36
3,00
3,50
4,79
5,40


8
1,86
2,31
2,90
3,36
4,50
5,04


9
1,83
2,26
2,82
3,25
4,30
4,70


10
1,81
2,23
2,76
3,17
4,14
4,59


11
1,80
2,28
2,72
3,11
4,03
4,44


12
1,78
2,18
2,68
3,05
3,93
4,32


13
1,77
2,16
2,65
3,01
3,85
4,22


14
1,76
2,14
2,62
2,98
3,79
4,14


15
1,75
2,13
2,60
2,95
3,73
4,07


16
1,75
2,12
2,58
2,92
3,69
4,01


17
1,74
2,11
2,57
2,90
3,65
3,96


18
1,73
2,10
2,55
2,88
3,61
3,92


19
1,73
2,09
2,54
2,86
3,58
3,88


20
1,73
2,09
2,53
2,85
3,55
3,85


21
1,72
2,08
2,52
2,83
3,53
3,82


22
1,72
2,07
2,51
2,82
3,51
3,79.


23
1,71
2,07
2,50
2,81
3,49
3,77


24
1,71
2,06
2,49
2,80
3,47
3,74


25
1,71
2,06
2,49
2,79
3,45
3,72


26
1,71
2,06
2,48
2,78
3,44
3,71


27
1,71
2,05
2,47
2,77
3,42
3,69


28
1,70
2,05
2,46
2,76
3,40
3,66


29
1,70
2,05
2,46
2,76
3,40
3,66


30
1,70
2,04
2,46
2,75
3,39
3,65


40
1,68
2,02
2,42
2,70
3,31
3,55


60
1,07
2,00
2,39
2,66
3,23
3,46


120
1,66
1,98
2,36
2,62
3,17
3,37




Приложение
3
Таблица
функции Лапласа










































































































































































































































































































































































































































































z
0
1
2
3
4
5
6
7
8
9


0,0
0,00000
0,00399
0,00798
0,01197
0,01595
0,01994
0,02392
0,02790
0,03188
0,03586


0,1.
0,03983
0,04380
0,04776
0,05172
0,05567
0,05962
0,06356
0,06749
0,07142
0,07535


0,2
0,07926
0,08317
0,08706
0,09095
0,09483
0,09871
0,10257
0,10642
0,11026
0,11409


0,3
0,11791
0,12172
0,12552
0,12930
0,13307
0,13683
0,14058
0,14431
0,14803
ОП5173


0,4
0,15542
0,15910
0,16276
0,16640
0,17003
0,17364
0,17724
0,18082
0,18439
0,18793


0,5
0,19146
0,19497
0,19847
0,20194
0,20540
0,20884
0,21226
0,21566
0,21904
0,22240


0,6
0,22575
0,22907
0,23237
0,23565
0,23891
0,24215
0,24537
0,24857
0,25175
0,25490


0,7
0,25804
0,26115
0,26424
0,26730
0,27035
0,27337
0,27637
0,27935
0,28230
0,28524


0,8
0,28814
0,29103
0,29389
0,29673
0,29955
0,30234
0,30511
0,30785
0,31057
0,31327


0,9
0,31594
0,31859
0,32121
0,32381
0,32639
0,32894
0,33147
0,33398
0,33646
0,33891


1,0
0,34134
0,34375
0,34614
0,34849
0,35083
0,35314
0,35543
0,35769
0,35993
0,36214


1,1
0,36433
0,36650
0,36864
0,37076
0,37286
0,37493
0,37698
0,37900
0,38100
0,38298


1,2
0,38493
0,38686
0,38877
0,39065
0,39251
0,39435
0,39617
0,39796
0,39973
0,40147


1,3
0,40320
0,40490
0,40658
0,40824
0,40988
0,41149
0,41308
0,41466
0,41621
0,41774


1,4
0,41924
0,42073
0,42220
0,42364
0,42507
0,42647
0,42785
0,42922
0,43056
0,43189


1,5
0,43319
0,43448
0,43574
0,43699
0,43822
0,43943
0,44062
0,44179
0,44295
0,44408


1,6
0,44520
0,44630
0,44738
0,44845
0,44950
0,45053
0,45154
0,45254
0,45352
0,45449


1,7
0,45543
0,45637
0,45728
0,45818
0,45907
0,45994
0,46080
0,46164
0,46246
0,46327


1,8
0,46407
0,46485
0,46562
0,46638
0,46712
0,46784
0,46856
0,46926
0,46995
0,47062


1,9
0,47128
0,47193
0,47257
0,47320
0,47381
0,47441
0,47500
0,47558
0,47615
0,47670


2,0
0,47725
0,47778
0,47831
0,47882
0,47932
0,47982
0,48030
0,48077
0,48124
0,48169


2,1
0,48214
0,48257
0,48300
0,48341
0,48382
0,48422
0,48461
0,48500
0,48537
0,48574


2,2
0,48610
0,48645
0,48679
0,48713
0,48745
0,48778
0,48809
0,48840
0,48870
0,48899


2,3
0,48928
0,48956
0,48983
0,49010
0,49036
0,49061
0,49086
0,49111
0,49134
0,49158


2,4
0,49180
0,49202
0,49224
0,49245
0,49266
0,49286
0,49305
0,49324
0,49343
0,49361


2,5
0,49379
0,49396
0,49413
0,49430
0,49446
0,49461
0,49477
0,49492
0,49506
0,49520


2,6
0,49534
0,49547
0,49560
0,49573
0,49585
0,49598
0,49609
0,49621
0,49632
0,49643


2,7
0,49653
0,49664
0,49674
0,49683
0,49693
0,49702
0,49711
0,49720
0,49728
0,49736


2,8
0,49744
0,49752
0,49760
0,49767
0,49774
0,49781
0,49788
0,49795
0,49801
0,49807


2,9
0,49813
0,49819
0,49825
0,49831
0,49836
0,49841
0,49846
0,49851
0,49856
0,49861


3,0
0,49865
0,49869
0,49874
0,49878
0,49882
0,49886
0,49889
0,49893
0,49896
0,49900


3,1
0,49903
0,49906
0,49910
0,49913
0,49916
0,49918
0,49921
0,49924
0,49926
0,49929


3,2
0,49931
0,49934
0,49936
0,49938
0,49940
0,49942
0,49944
0,49946
0,49948
0,49950


3,3
0,49952
0,49953
0,49955
0,49957
0,49958
0,49960
0,49961
0,49962
0,49964
0,49965


3,4
0,49966
0,49968
0,49969
0,49970
0,49971
0,49972
0,49973
0,49974
0,49975
0,49976


3,5
0,49977
0,49978
0,49978
0,49979
0,49980
0,49981
0,49981
0,49982
0,49983
0,49983


3,6
0,49984
0,49985
0,49985
0,49986
0,49986
0,49987
0,49987
0,49988
0,49988
0,49989


3,7
0,49989
0,49990
0,49990
0,49990
0,49991
0,49991
0,49992
0,49992
0,49992
0,49992


3,8
0,49993
0,49993
0,49993
0,49994
0,49994
0,49994
0,49994
0,49995
0,49995
0,49995


3,9
0,49995
0,49995
0,49996
0,49996
0,49996
0,49996
0,49996
0,49996
0,49997
0,49997


4,0
0,499968


4,5
0,49997


5,0
0,4999997



Приложение
4
Критические
точки распределения Фишера-Снедекора































































































































































































































Уровень
значимости а = 0,01


1
161
200
216
225
230
234
237
239
241
242
243
244


2
18,51
19,00
19,16
19,25
19,30
19,33
19,36
19,37
19,38
19,39
19,40
19,41


3
10,13
9,55
9,28
9,12
9,01
8,94
8,88
8,84
8,81
8,78
8,76
8,74


4
7,71
6,94
6,59
6,39
6,26
6,16
6,09
6,04
6,00
5,96
5,93
5,91


5
6,61
5,79
5,41
5,19
5,05
4,95
4,88
4,82
4,78
4,74
4,70
4,68


6
5,99
5,14
4,76
4,53
4,39
4,28
4,21
4,15
4,10
4,06
4,03
4,00


7
5,59
4,74
4,35
4,12
3,97
3,87
3,79
3,73
3,68
3,63
3,60
3,57


8
5,32
4,46
4,07
3,84
3,69
3,58
3,50
3,44
3,39
3,34
3,31
3,28


9
5,12
4,26
3,86
3,63
3,48
3,37
3,29
3,23
3,18
3,13
3,10
3,07


10
4,96
4,10
3,71
3,48
3,33
3,22
3,14
3,07
3,02
2,97
2,94
2,91


11
4,84
3,98
3,59
3,36
3,20
3,09
3,01
2,95
2,90
2,86
2,82
2,79


12
4,75
3,88
3,49
3,26
3,11
3,00
2,92
2,85
2,80
2,76
2,72
2,69


13
4,67
3,80
3,41
3,18
3,02
2,92
2,84
2,77
2,72
2,67
2,63
2,60


14
4,60
3,74
3,34
3,11
2,96
2,85
2,77
2,70
2,65
2,60
2,56
2,53


15
4,54
3,68
3,29
3,06
2,90
2,79
2,70
2,64
2,59
2,55
2,51
2,48


16
4,49
3,63
3,24
3,01
2,85
2,74
2,66
2,59
2,54
2,49
2,45
2,42


17
4,45
3,59
3,20
2,96
2,81
2,70
2,62
2,55
2,50
2,45
2,41
2,38