Исходные данные
о продаже квартир на вторичном рынке жилья












№ п/п
y

x1


x2

Задание



1
2
					







3
4
5
6
7
8
9
10
11
12
13
14
15
16


22.5
26
18.5
13.2
25.8
17
18
21
14.5
23
19.5
14.2
13.3
16.1
13.516


29
35
28
30
51
38
30
32
27
39
29.5
29
30
30.8
28
31


15
10
10
25
10
12
15
20
10
5
15
12
5
10
25
10


y – цена квартиры
(тыс.$);
x1 – жилая площадь(кв.
м);
x2 – время пути до метро
(мин).
По имеющимся
статистическим данным
отдельно для пар (у,х1)
и (у,х2) найти:
а) уравнение линейной
регрессии;
б) коэффициент
корреляции;
в) среднюю величину у при
х1=35 (х2=12);
г) 95% доверительные
интервалы для
индивидуального и
среднего значения у;
д) с надежностью 0.95
интервальные оценки коэффициента регрессии b1 и дисперсии s2;
е) коэффициент
детерминации.
Оценить на уровне 0.05
значимость
уравнения регрессии.
Сделать анализ
полученных результатов.





Табличные
значения стандартных функций распределения:
t0.05,14 = 2.145 F0.05,1,14 = 4.6
c20.025,14 =26.1 c20.975,14 =5.63
1. Парная
регрессия y на
x1. 
а) Найти
уравнение линейной регрессии для x1.

























































































































































№ п/п


yi


xi


y2


x2


x * y


xi –   


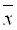
(xi –  )2



1
22,5
29
506,25
841
652,5
 — 3,3
10,89


2
26
35
676
1225
910
2,7
7,29


3
18,5
28
342,25
784
518
 — 4,3
18,49


4
13,2
30
174,24
900
396
 — 2,3
5,29


5
25,8
51
665,64
2601
1315,8
18,7
349,69


6
17
38
289
1444
646
5,7
32,49


7
18
30
324
900
540
2,3
5,29


8
21
32
441
1024
672
 — 0,3
0,09


9
14,5
27
210,25
729
391,5
 — 5,3
28,09


10
23
39
529
1521
897
6,7
44,89


11
19,5
29,5
380,25
870,25
575,25
 — 2,8
7,84


12
14,2
29
201,64
841
411,8
 — 3,3
10,89


13
13,3
30
176,89
900
399
 — 2,3
5,29


14
16,1
30,8
259,21
948,64
495,88
 — 1,5
2,25


15
13,5
28
182,25
784
378
 — 4,3
18,49


16
16
31
256
961
496
 — 1,3
1,69


Сумма
292,1
517,3
5613,87
17273,89
9694,73
548,95


Средняя
18,2
32,3
350,9
1079,6
605,9
34,3




Таким
образом, выборочные средние значения  = 32,3;  = 18,2;  = 605,9;
выборочная
дисперсия  = 34,3;
выборочная
ковариация cov(x,y) =  = 605,9-32,3*18,2 = 18,04;
Коэффициенты
регрессии b1=  =  = 0,53
  = 18,2 – 0,53*32,3 = 1,08
При
увеличении жилой площади на 1 кв.м цена квартиры в среднем возрастает на 0,53
тыс.$.
Уравнение
регрессии  = 1,08 + 0,53 * x.
б) рассчитать
коэффициент корреляции
  
  
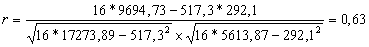
Между величиной
жилой площади квартиры и ценной квартиры наблюдается умеренная положительная
зависимость.
в) определить
среднюю величину y при x1=35.
  
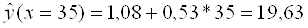
Средняя цена
квартиры при жилой площади 35 кв.м составляет 19.63 тыс.$. Промежуточные
вычисления для последующих расчетов проводим в таблице.




















































































































































№ п/п


yi


xi


  


  


  


  


  




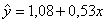
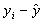
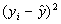
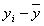
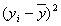
1

22,5
29
16.45
6.05
36.60
4.3
18.49



2

26
35
19.63
6.37
40.58
7.8
60.84



3

18,5
28
15.92
2.58
6.66
0.3
0.09



4

13,2
30
16.98
 — 3.78
14.29
 — 5.0
25.00



5

25,8
51
28.11
 — 2.31
5.34
7.6
57.76



6

17
38
21.22
 — 4.22
17.81
 — 1.2
1.44



7

18
30
16.98
1.02
1.04
 — 0.2
0.04



8

21
32
18.04
2.96
8.76
2.8
7.84



9

14,5
27
15.39
 — 0.89
0.79
 — 3.7
13.69



10

23
39
21.75
1.25
1.56
4.8
23.04



11

19,5
29,5
16.72
2.78
7.73
1.3
1.69



12

14,2
29
16.45
 — 2.25
5.06
 — 4.0
16.00



13

13,3
30
16.98
 — 3.68
13.54
 — 4.9
24.01



14

16,1
30,8
17.40
 — 1.30
1.69
 — 2.1
4.41



15

13,5
28
15.92
 — 2.42
5.86
 — 4.7
22.09



16

16
31
17.51
 — 1.51
2.28
 — 2.2
4.84



Сумма

292,1
517,3
169.59
281.27



Средняя

18,2
32,3
17.58




г) найти 95%
доверительные интервалы для индивидуального и среднего значения y.
С учетом
значений из обеих таблиц:
Остаточная
дисперсия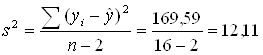  
Дисперсия
среднего значения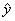     
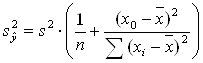
   = 0.920
Стандартное
отклонение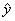   
Дисперсия
индивидуального значения y0  
  
Стандартное
отклонение y0   
Для
доверительной вероятности g=0,95 уровень значимости a = 1-g = 0,05.
Табличное
значение t-распределения
Стьюдента для уровня значимости a = 0,05 и числа степеней
свободы k
= n — 2 =16-2 =14 составляет t0.05,8 = 2,31.
Доверительный
интервал для среднего значения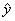  
  
19.63 – 2.145×0.96 £ y £ 19.63 + 2.145×0.96
17.57£ y £ 21.69
Доверительный
интервал для индивидуального значения  
  
19.63 – 2.145×3.61 £ y0 £ 19.63 + 2.145×3.61
11.89 £ y0 £ 27.37
С
учетом возможных ошибок средняя цена квартиры с площадью 35 кв.м с вероятностью
95% лежит в пределах от 17,57 до 21,69 тыс.$; при этом отдельно цена квартиры
колебаться от 11,89 до 27,37 тыс.$.
д) с
надежностью 0,95 найти интервальные оценки коэффициента регрессии b1 и дисперсии возмущений s2.
Дисперсия
коэффициента регрессии  =  = 0.022
Стандартное
отклонение  
Доверительный
интервал для коэффициента регрессии b1
  
0.53–2.145×0.148 £ b1 £ 0.53+ 2.145×0.148
0.21 £ b1 £ 0.85
С надежностью
0,95 увеличение площади квартиры на 1 кв.м приводит к увеличению цены квартиры
на величину от 0,21 до 0,85 тыс.$.
Табличные
значения распределения c2 Пирсона для уровня значимости 0,05 и числа
степеней свободы 14 составляют
  ;  
Доверительный
интервал дисперсии возмущений 
  
  
7,42 £ s2 £ 34,42
Интервал для
стандартного отклонения 2,72 £ s £ 5,87.
С
надежностью 0,95 дисперсия ошибок расчета находится в пределах от 7,42 до
34,42, а стандартное отклонение цены квартиры от среднего значения лежит в
пределах от 2,72 до 5,87.
Оценить на
уровне 0,05 значимость уравнения регрессии.
Общая сумма
квадратов отклонений y  = 281,27
Остаточная
сумма квадратов  = 169,59
Сумма
квадратов, объясненная регрессией  =
281,27–169,59 = 111,68
Величина F-критерия
  = 9,23,
где m – число параметров
(коэффициентов), рассчитанных по уравнению регрессии m=2.
Табличное
значение F-распределения
Фишера для уровня значимости a=0,05 и числа степеней свободы k1=n-m=14 и k2=m — 1=1 составляет F0,05,1,14=4,6.
Так как
расчетное значение F-критерия больше табличного критического, то уравнение регрессии y по x1 следует признать
значимым, т.е. заслуживающим доверия.
Определим
коэффициент детерминации.
  0,40
Вариация
зависимой переменной (цены квартиры) на 40% определяется фактором x –площадью квартиры.
2. Парная
регрессия y на
x2. 
а) Найти
уравнение линейной регрессии для x2.

























































































































































№ п/п


yi


xi


y2


x2


x * y


xi –
  


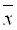
(xi –  )2



1
22,5
15
506,25
225
337,5
1,9
3,61


2
26
10
676
100
260
 — 3,1
9,61


3
18,5
10
342,25
100
185
 — 3,1
9,61


4
13,2
25
174,24
625
330
11,9
141,61


5
25,8
10
665,64
100
258
 — 3,1
9,61


6
17
12
289
144
204
 — 1,1
1,21


7
18
15
324
225
270
1,9
3,61


8
21
20
441
400
420
6,9
47,61


9
14,5
10
210,25
100
145
1,9
3,61


10
23
5
529
25
115
 — 8,1
65,61


11
19,5
15
380,25
225
292,5
1,9
3,61


12
14,2
12
201,64
144
170,4
 — 1,1
1,21


13
13,3
5
176,89
25
66,5
 — 8,1
65,61


14
16,1
10
259,21
100
161
 — 3,1
9,61


15
13,5
25
182,25
625
337,5
11,9
141,61


16
16
10
256
100
160
 — 3,1
9,61


Сумма
292,1
209
5613,87
3263
3712,4
526,96


Средняя
18,2
13,1
350,9
203,94
232,025
32,9




Таким
образом, выборочные средние значения  = 13,1;  = 18,2;  = 232,025;
выборочная
дисперсия  = 32,9;
выборочная
ковариация cov(x,y) =  = 232,025-13,1*18,2 = — 6,4;
Коэффициенты
регрессии b1=  =  = — 0,19 
  = 18,2 – ( — 0,19)*13,1 = 20,7
При
увеличении времени пути до метро на 1 мин. цена квартиры в среднем снижается на
0,19 тыс.$.
Уравнение
регрессии  = 20,7 – 0,19 * x.
б) рассчитать
коэффициент корреляции
  
  
Между временем
пути до метро от квартиры и ценной квартиры наблюдается слабая отрицательная
зависимость.
в) определить
среднюю величину y при x2=12.
  
Средняя цена
квартиры при времени пути до метро 12 минут составляет 19.63 тыс.$.
Промежуточные
вычисления для последующих расчетов проводим в таблице




















































































































































№ п/п


yi


xi


  


  


  


  


  




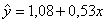
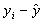
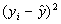
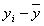
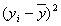
1

22,5
15
17,85
4,65
21,62
4.3
18.49



2

26
10
18,80
7,2
51,84
7.8
60.84



3

18,5
10
18,80
 — 0,3
0,09
0.3
0.09



4

13,2
25
15,95
 — 2,75
7,56
 — 5.0
25.00



5

25,8
10
18,80
7,0
49,0
7.6
57.76



6

17
12
18,42
 — 1,42
2,02
 — 1.2
1.44



7

18
15
17,85
0,15
0,02
 — 0.2
0.04



8

21
20
16,90
4,1
16,81
2.8
7.84



9

14,5
10
18,80
 — 4,3
18,49
 — 3.7
13.69



10

23
5
19,75
3,25
10,56
4.8
23.04



11

19,5
15
17,85
1,65
2,72
1.3
1.69



12

14,2
12
18,42
 — 4,22
17,81
 — 4.0
16.00



13

13,3
5
19,75
 — 6,45
41,60
 — 4.9
24.01



14

16,1
10
18,80
 — 2,7
7,29
 — 2.1
4.41



15

13,5
25
15,95
 — 2,45
6,003
 — 4.7
22.09



16

16
10
18,80
 — 2,8
7,84
 — 2.2
4.84



Сумма

292,1
209
261,27
281.27



Средняя

18,2
13,1
17.58




г) найти 95%
доверительные интервалы для индивидуального и среднего значения y.
С учетом
значений из обеих таблиц:
Остаточная
дисперсия  
Дисперсия
среднего значения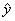     
   = 1,21
Стандартное
отклонение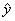   
Дисперсия
индивидуального значения y0  
  
Стандартное
отклонение y0   
Для
доверительной вероятности g=0,95 уровень значимости a = 1-g = 0,05.
Табличное
значение t-распределения
Стьюдента для уровня значимости a = 0,05 и числа степеней
свободы k
= n — 2 =16-2 =14 составляет t0.05,8 = 2,31.
Доверительный
интервал для среднего значения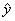  
  
18,42 – 2,145×1,1 £ y £ 18,42 + 2,145×1,1
16,06£ y £ 20,78
Доверительный
интервал для индивидуального значения  
  
18,42 – 2,145×4,46 £ y0 £ 18,42 + 2,145×4,46
8,85 £ y0 £ 27,99
С
учетом возможных ошибок средняя цена квартиры с временем пути до метро 12 минут
с вероятностью 95% лежит в пределах от 16,06 до 20,78 тыс.$; при этом отдельно
цена квартиры колебаться от 8,85 до 27,99 тыс.$.
д) с
надежностью 0,95 найти интервальные оценки коэффициента регрессии b1 и дисперсии возмущений s2.
Дисперсия
коэффициента регрессии  =  = 0.035
Стандартное
отклонение  
Доверительный
интервал для коэффициента регрессии b1
  
 — 0,19–2,145×0,187 £ b1 £ — 0,19 + 2,145×0,187
0,59£ b1 £ 0,21
С надежностью
0,95 увеличение времени пути до метро на 1 минуту приводит к увеличению цены
квартиры на величину от – 0,59 до 0,21 тыс.$.
Табличные
значения распределения c2 Пирсона для уровня значимости 0,05 и числа
степеней свободы 14 составляют
  ;  
Доверительный
интервал дисперсии возмущений 
  
  
11,44 £ s2 £ 53,03
Интервал для
стандартного отклонения 3,38 £ s £ 7,28.
С
надежностью 0,95 дисперсия ошибок расчета находится в пределах от 11,44 до
53,03, а стандартное отклонение цены квартиры от среднего значения лежит в
пределах от 3,38 до 7,28.
Оценить на
уровне 0,05 значимость уравнения регрессии.
Общая сумма
квадратов отклонений y  = 281,27
Остаточная
сумма квадратов  = 261,27
Сумма
квадратов, объясненная регрессией  =
281,27–261,27 = 20
Величина F-критерия
  = 1,07,
где m – число параметров
(коэффициентов), рассчитанных по уравнению регрессии m=2.
Табличное
значение F-распределения
Фишера для уровня значимости a=0,05 и числа степеней свободы k1=n-m=14 и k2=m — 1=1 составляет F0,05,1,14=4,6.
Так как
расчетное значение F-критерия больше табличного критического, то уравнение регрессии y по x1 следует признать
значимым, т.е. заслуживающим доверия.
Определим
коэффициент детерминации.
квартира
стоимость регрессия вариация
  0,07
Вариация
зависимой переменной (цены квартиры) на 7% определяется фактором x –временем пути до метро.