Задача №1
Работа
двадцати предприятий пищевой промышленности
В отчетном
периоде характеризуется следующими данными:
Таблица 1

































































№
					









1


2




1


10


11,8




2


11


12,4




3


12,6


13,8




4


13


15,1




5


14,2


16,4




6


15


17




7


15,5


17,3




8


16,3


18,1




9


17,7


19,6




10


19,3


23,1




11


10,8


12




12


12,2


13




13


12,8


12,9




14


13,5


15,6




15


14,6


16,8




16


15,3


18,2




17


16


17,9




18


17,1


10




19


18


18




20


20


27,2




1-Среднегодовая стоимость
промышленно-производственных ОФ, млн. руб.
2-Товарная продукция в
сопоставимых оптовых ценах предприятия, млн. руб.
1. 
Проведите
ранжирование исходных данных по размеру ОФ и их группировку, образовав 5 групп
с равновеликими интервалами. Приведите расчет равновеликого интервала
группировки по формуле:
H=Xmax-Xmin/n
2. 
Определите
по каждой группе:
– число
заводов;
– стоимость
ОПФ-всего и в среднем на один завод:
– стоимость
ТП-всего и в среднем на один завод.
Результаты представьте
в табличном виде, проанализирйте их и сделайте выводы
H=20–10/5=2
где xmax, xmin – максимальное и
минимальное значения кредитных вложений
Определим
теперь интервалы групп (xi, xi+1):
1 группа: 10–12
млн. руб.
2 группа: 12–14
млн. руб.
3 группа: 14–16
млн. руб.
4 группа: 16–18
млн. руб.
5 группа: 18–20
млн. руб.
Далее
упорядочим исходную таблицу по возрастанию ОФ























































№
Группа
Среднегодовая стоимость
промышленно – производственных ОФ в группе, млн. руб.
Товарная продукция в
сопоставимых оптовых ценах предприятия, млн. руб.


1
10,1–12
10
11,8


11
12,4


10,8
12


2
12,1–14
12,6
13,8


13
15,1


12,2
13


12,8
12,9


13,5
15,6


3
14,1–16
14,2
16,4


15
17


15,5
17,3


14,6
16,8


15,3
18,2


16
17,9


4
16,1–18
16,3
18,1


17,7
19,6


17,1
10


18
18


5
18,1–20
19,3
23,1


20
27,2



На основе
полученной таблицы определим требуемые показатели. Результаты представим в виде
групповой таблицы:
Таблица 1.2





























































Группа
Количество заводов в
группе, шт.
Среднегодовая стоимость
промышленно – производственных ОПФ, млн. руб.
Стоимость промышленно –
производственных ОПФ, млн. руб.
Товарная продукция в
сопоставимых оптовых ценах предприятия, млн. руб.


1
3
10–12
Всего
31,8
Всего
36,2


В среднем на один завод
10,6
В среднем на один завод
12,067


2
5
12,1–14
Всего
64,1
Всего
70,4


В среднем на один завод
12,82
В среднем на один завод
14,08


3
6
14,1–16
Всего
90,6
Всего
103,6


В среднем на один завод
15,1
В среднем на один завод
17,27


4
4
16,1–18
Всего
69,1
Всего
65,7


В среднем на один завод
17,275
В среднем на один завод
17,275


5
2
18,1–20
Всего
39,3
Всего
50,3


В среднем на один завод
19,65
В среднем на один завод
25,15



Задача №4
Имеются
данные по трем предприятиям, вырабатывающие однородную продукцию:























№
Базисный год
Отчетный год


Затрата времени на ед.
продукции, час
Выпущено продукции,
тыс. ед.
Затраты времени на ед.
продукции, тыс. ед.
Затраты времени на всю
продукцию, ч


1
0,34
52,1
0,34
19975


2
0,48
45,7
0,48
22248


3
0,53
23,8
0,53
13462



Обоснуйте
выбор формул средней и по этим формулам определите средние затраты времени на
продукцию по трем предприятиям в базисном и отчетном годах, сравните полученные
результаты и сделайте выводы.


Решение
Средние
затраты времени определяются по формуле:
  ,
где V – затраты времени на
единицу продукции; S – затраты времени на всю продукцию. Определим
средние затраты времени на 3 предприятиях. Т.к. заданы затраты времени на
единицу продукции и затраты времени на всю продукцию то:
  
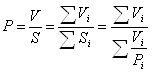
Данная
формула называется средней гармонической взвешенной.
Подставив в
последнюю формулу известные значения, получим средние затраты времени на
производство на предприятиях в отчетном году:
P=19975+22248+13462/(19972/0,34+22248/0,48+13462/0,53)= 0,427 ч
Определим
средние затраты времени на производства продукции в базисном году:
  
Данная
формула называется средней арифметической взвешенной.
Подставив в
последнюю формулу известные значения, получим затраты времени на производство
продукции в базисном году:
P=(0,34*52,1+0,48*45,7+0,53*23,8)/(52,1+45,7+23,8)= 0,4298=0,43 ч
Вывод:
средние затраты времени на производство продукции в базисном и отчетном году
отличаются на (0,43–0,427)*100%= 0,003*100%=0,3%
Задача №9
В результате
контрольной выборочной проверки расфасовки чая осуществлена 25% механическая
выборка по способу бесповторного отбора, в результате которой получено
следующее распределение пачек чая по массе:















Масса пачки чая, г
Число пачек чая, шт.


До 49
17


49–50
52


50–51
21


51–52
7


52 и выше
3


ИТОГО
100



По
результатам выборочного обследования определите:
1. 
Среднюю
массу пачки чая;
2. 
Дисперсию
и среднее квадратичное отклонение;
3. 
Коэффициент
вариации;
4. 
С
вероятностью 0,997 возможные пределы средней массы пачки чая во всей партии продукции;
5. 
С
вероятностью 0,954 возможные пределы удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции.
Решение
Приведем группировку к стандартному виду с равными
интервалами и найдем середины интервалов для каждой группы. Результаты
представлены в таблице:



























Масса пачки чая, г
Масса пачки чая, г
Средняя масса пачки
чая, г
Число пачек чая, шт


До 49
48–49
48,5
17


От 49 до 50
49–50
49,5
52


От 50 до 51
50–51
50,5
21


От 51 до 52
51–52
51,5
7


Свыше 52
52–53
52,5
3


Итого
100



Среднюю массу
пачки чая находим по формуле средней арифметической взвешенной:
  
Подставив в последнюю формулу известные значения, получим
среднюю массу пачки чая:
Y=(48.5*17+49.5*52+50.5*21+51.5*7+52.5*3)/100=49.77 г.
Дисперсия
определяется по формуле:
  .
Подставив в
последнюю формулу известные значения, получим дисперсию:
s²=((48,5–49,77)²*17+(49,5–49,77)²*52+(50,5–49,77)²*21+(51,5–49,77)²*7+(52,5–49,77)²)/100=85,71/100=0,8571
г.²
Среднее
квадратическое отклонение равно:
S=√s²=√0,8571=0,93
г.
Коэффициент
вариации определяется по формуле:
V=s/y=0,93/49,77= 0,019*100%=1,9%
Рассчитаем
сначала предельную ошибку выборки. Так при вероятности p = 0,997 коэффициент
доверия t = 3. Поскольку дана 25%-ная случайная
бесповторная выборка, то
n/N=0,25
где n – объем выборочной
совокупности, N – объем генеральной совокупности.
Считаем
также, что дисперсия s²=0,8571. Тогда предельная ошибка выборочной средней
равна:
Δy=t*√σ²/n*(1-n/N)=3*√0,8571/100*(1–0,25)=0,24
г.
Определим
теперь возможные границы, в которых ожидается средняя масса чая на 1 пакетик
чая
y – Δy≤my≤y+ Δy
49,77–0,8571≤my≤49,77+0,8571
48,9129≤my≤50,6271
Т.е., с
вероятностью 0,997 можно утверждать, что масса чая на 1 пакетик находится в
пределах 48,9129 до 50,6271
Выборочная
доля w удельного веса пачек чая с массой до 49 г. и свыше 52 г. во всей продукции с вероятностью 0,954 равна.
W=(48+3)/100=0,51=51 г.
Учитывая, что
при вероятности p = 0,954 коэффициент доверия t = 2, вычислим
предельную ошибку выборочной доли:
Δw= t*√(w*(1-w)/n) *(1-n/N)=2*√(0,51*(1–0,51)/100)*(1–0,25)=0,086г
или
Пределы доли
признака во всей совокупности:
51–8,6≤d≤51+8,6
42,4≤d≤59,6
Таким
образом, с вероятностью 0,954 можно утверждать, что границы удельного веса
пачек чая находятся в пределах42,4г до 59,6г во всей продукции.
Выводы:
1. 
Так
как коэффициент вариации меньше 33%, то исходная выборка однородная.
Задача №14
Урожайность
пшеницы характеризуется следующими данными.
Интервальный
ряд динамики «А»
















года
показатель

1992
1993
1994
1995
1996
1997


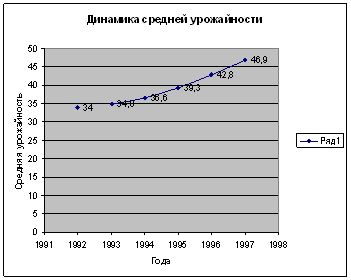
Средняя урожайность,
ц/га
34
34,8
36,6
39,3
42,8
46,9



На основе
имеющихся данных:
1. 
Определите
все аналитические показатели ряда динамики «А»
2. 
Покажите
взаимосвязь цепных и базисных темпов роста
3. 
Приведите
графическое изображение динамики средней урожайности
Моментальный
ряд динамики» Б»












дата
показатель

На 1.1
На 1.2
На 1.3
На 1.4


Списочная
численность рабочих, чел.
402
406
403
408



4. 
Приведите
расчет среденесписочной численности работников предприятия за квартал по данным
моментального ряда динамики» Б» по формуле средней хронологической для
моментального ряда.


Решение
1. Определим
показатели, характеризующие рост урожайности пшеницы: абсолютные приросты,
темпы роста и прироста по годам. Формулы для расчета следующие.
Определим
абсолютный прирост цепным способом:
Δy=yi-yi — 1
1993=34,8–34=0,8
1994=36,6–34,8=1,8
1995=39,3–36,6=2,7
1996=42,8–39,3=3,5
1997=46,9–42,8=4,1
Базисным
способом
Δy=yi-y0
1993=34,8–34=0,8
1994=36,6–34=2,6
1995=39,3–34=5,3
1996=42,8–34=8,8
1997=46,9–34=12,9
Определим
темпы прироста цепным способом
Tр.ц= yi/ yi — 1*100%
1993=34,8/34*100%=102,36%
1994=36,6/34,8*100%=105,17%
1995=39,3/36,6*100%=107,38%
1996=42,8/39,3*100%=108,91
1997=46,9/42,8*100%=109,58%
Базисным
способом
1993=34,8/34*100%=102,36%
1994=36,6/34*100%=107,65%
1995=39,3/34*100%=115,59%
1996=42,8/34*100%=125,88%
1997=46,9/34*100%=137,94%
Определим
темпы прироста цепным способом
Тпр.ц=Трц — 100%
1993=102,36% — 100%=2,36%
1994=105,17% — 100%=5,17%
1995=107,38% — 100%=7,38%
1996=108,91% — 100%=8,91%
1997=109,58% — 100%=9,58%
Базисным
способом
Тпр б=Тр б — 100%
1993=102,36% — 100%=2,36%
1994=107,65% — 100%=7,65%
1995=115,59% — 100%=15,59%
1996=125,88% — 100%=25,88%
1997=137,94% — 100%=37,94%
Определим
абсолютное значение 1%
1993=34*0,01=0,34
1994=34,8*0,01=0,348
1995=36,6*0,01=0,366
1996=39,3*0,01=0,393
1997=42,8*0,01=0,428
Результаты
приведены в таблице:


































































Годы
Средняя урожайность пшеницы,
ц/га
Абсолютный прирост,
млрд. руб.
Темпы роста, %
Темпы прироста, %
Абсолютное содержание 1%
прироста


по годам
по годам
по годам


1992
34
цепной
базисный
цепной
базисный
цепной
базисный


—
—
—


1993
34,8
0,8
0,8
102,36
102,35
2,36
2,36
0,34


1994
36,6
1,8
2,6
105,17
107,52
5,17
7,65
0,348


1995
39,3
2,7
5,3
107,38
114,9
7,38
15,59
0,366


1996
42,8
3,5
8,8
108,91
123,5
8,91
25,88
0,393


1997
46,9
4,1
12,9
109,58
133,08
9,58
37,94
0,428



Среднегодовую
урожайность пшеницы определим по формуле средней арифметической взвешенной:
Х=(34+34,8+36,6+39,3+42,8+46,9)/6=234,4/6=39,066
  
Для
моментального ряда «Б» с равностоящими уровнями средний уровень ряда можно
вычислить по формуле средней хронологической:
Y=(1/2Y0+Y1+Y2+…1/2Yn)/n — 1
Y=(1/2*402+406+403+1/2408)/4–1=405
человек
Среднесписочная
численность рабочих за 1 квартал составила 405 человек.
Задача №19
Себестоимость
и объем производства Советского шампанского характеризуется следующими данными:


















Марка шампанского
Себестоимость 100
бутылок, руб.
Выработано продукции,
тыс. бутылок


ноябрь
декабрь
ноябрь
декабрь


Полусладкое
2233
2222
1835
1910


Сладкое
1725
1716
1404
1415




Определите:
1. 
Индивидуальные
и общие индексы себестоимости продукции.
2. 
Общий
индекс затрат на продукцию (издержек производства)
3. 
Использую
взаимосвязь индексов, определите, на сколько% увеличивается объем производства
продукции
Решение
Общий индекс
себестоимости продукции:
Iz=(∑Z1*q1)/(∑Z0q1)
Где Z1, Z0 – себестоимость единицы
продукции в ноябре и декабре;
Где q1, q0 – физический объем
продукции в ноябре и декабре.
Iz=(2222*1910+1415*1716)/(2233*1910+1725*1415)=
0,994968
Общий индекс
физического объема продукции:
Iq=(∑Z0* q1)/ (∑Z0q0)
Iq=(2233*1910+1725*1415)/(2233*1835+1725*1404)=
1,028599
Общий индекс
затрат на производство продукции:
Izq= (∑Z1*q1)/(∑Z0q0)=(2222*1910+1415*1716)/(2233*1835+1725*1404)=
1,023423
Взаимосвязь
индексов: Izq= Iz* Iq 1,023423=1,028599*0,994968
Задача №24
Имеются
следующие данные по хлебозаводу:


















Виды продукции
Себестоимость
за 1 т, руб.
Продано продукции, т


Базисный
Отчетный
Базисный
Отчетный



Батоны столовые
в/с – 0,3 кг

38,8
40,1
1254
1210



Батоны нарезные
в/с – 0,5 кг

35,6
36,85
2565
2632



Вычислите:
1.  Индекс цен переменного
состава
2.  Индекс цен постоянного
состава
3.  Индекс структурных
сдвигов
4.  Покажите взаимосвязь между
исчисленными индексами.
5.  Поясните полученные
результаты.
Решение
Индекс
переменного состава:
Iсп=P1:P0=∑Р1q1/∑q1:∑ Р0q0/∑q0=∑Р1q1/∑q1*∑q0/∑ Р0q0
Где P1 и P0-соответсвенно средняя
цена в отчетном и базисном периодах.
Iсп=(40,1*1210+36,85*2565)*(3842/38,8–1254+35,6*2565)=1,033
Повышение
средней цены в отчетном периоде составило 3,3%, повышение средней
Цены может
быть вызвано повышением цен на отдельные виды продукции и ростом удельного веса
продукции с более высокой ценой.
Индекс цен
постоянного (фиксированного) состава:
Iфс=∑Р1q1/∑q1: ∑ Р0q1/∑q1=∑Р1q1/∑q1*∑q1/∑ Р0q1
Iфс=(40,1*1210+36,85*2632)/3842*(3842/38,8*1210+35,6*2632)=1,035
Индекс
структурных сдвигов:
Iстр=∑Р0q1/∑q1:∑ Р0q0/∑q0=(∑Р0q1/∑q1)*(∑q0/∑ Р0q0)
Iстр=(38,8*1210+35,6*2632)/3842*(3819/38,8*1254+35,6*2565)=0,998
Взаимосвязь
трех индексов:
Iсп= Iфс* Iстр
1,033=0,998*1,035
В среднем
цены на батоны в отчетном периоде повысились на 3,3%, за счет повышения цен на
отдельные виды батонов средние цены повысились на 3,5%, за счет изменения
структуры производства продукции по разным видам батонов цены снизились на 0,2%
Задача №29
Стоимость
фактически выпущенной продукции в действующих ценах составила:


















Вид продукции
Стоимость произведенной
продукции, тыс. руб.
Изменение цен в
отчетном по сравнению с базисным, %


Базисная
Отчетная


Макароны
104
106
+10


Вермишель
1616
1611
 — 5


Лапша
1038
1044
Без изменения



Исчислите:
1.  Общий индекс стоимость
продукции
2.  Индивидуальные и общие
индексы цен и абсолютную сумму экономии (или перерасхода) от изменения цен
3.  Общий индекс физического
объема продукции, используя взаимосвязь всех трех индексов
4.  Поясните полученные
результаты.
Iq=∑qi*p0/∑q0*p0
q1=ip*q0, тогда Iq= ip*q0*р0/∑q0*p0
Где Р0q0 – стоимость продукции в
базисном периоде, руб.;
Ip-индивидуальный индекс
объема продукции;













Виды продукции
Изменение количества
произведенной продукции в отчетном периоде по сравнению с базисным, %
Индивидуальный индекс
цен


Макароны
+10
Iq=(100+10)/100=1,1


Вермишель
 — 5
Iq=(100–5)/100=0,95


Лапша
Без изменения
Iq=(100–0)/100=1



Общий индекс
товарооборота в фактических ценах равен
  (106+1611+1044)/(104+1616+1038)=1,001
Общий индекс
цен равен
  2761/(106/1,1*1)+(1611/0,95*1)+(1044/1*1)=0,97
Общий индекс физического объема товарооборота,
используя взаимосвязь индексов, определим как:
  =1,001/0,97=1,032=103,2%
Выводы.
За отчетный год цены снизились на 3%.
За отчетный год физический объем товарооборота
вырос на 3,2%.
За отчетный год товарооборот в фактических ценах
вырос на 0,1%.