Выборка
банков
Таблица 1 – Список
30 крупнейших банков России по размеру капитала, млн. руб.





























































































































































Ранг

Название банка
Город
Чистые активы
Прибыль


1
Внешторгбанк
Москва
25286
1962


2
ОНЭКСИМбанк
Москва
19221
266


3
Инкомбанк
Москва
17275
744


4
Империал
Москва
6649
429


5
Международный
московский банк
Москва
7609
290


6
Международный промышленный
банк
Москва
4887
18


7
Российский кредит
Москва
12278
367


8
МЕНАТЕП
Москва
11058
146


9
Промстройбанк России
Москва
5651
239


10
Уникомбанк
Москва
3743
57


11
Возрождение
Москва
4079
158


12
Московский деловой мир
Москва
1951
340


13
Нефтехимбанк
Москва
2568
41


14
Ланта-банк
Москва
630
35


15
ИнтерТЭКбанк
Москва
1295
57


16
Гута-банк
Москва
5636
66


17
Совфинтрейд
Москва
1356
215


18
Совиндбанк
Москва
811
301


19
Русский банк имущественной
опеки
Москва
425
21


20
Чейз Манхеттен Банк
Интернэшил
Москва
2317
335


21
Еврофинанс
Москва
1283
96


22
Омскпромстройбанк
Омск
650
62


23
Запсибкомбанк
Тюмень
1137
133


24
Диалог-Банк
Москва
1012
127


25
Кредит Свисс АО
Москва
2869
118


26
МАПО-Банк
Москва
1237
5


27
Росэксимбанк
Москва
339
95


28
Уральский банк
реконструкции и развития
Екатеринбург
513
115


29
Уралтрансбанк
Екатеринбург
622
143


30
Пробизнесбанк
Москва
1486
88



Способ отбора
банков – механический. Я выбрал каждый второй банк.
a) 
1
Анализ выборочной совокупности
					







b) 
а) Количество
групп определяем по формуле Стерджесса:
n = 1+3,322 lg N
где: n – число групп;
N – число единиц
совокупности.
n=1+3,322 lg 30=5,906997≈6
Величина
интервала определяется по формуле:
h = (Xmax – Xmin) /n
где: Xmax – максимальное значение
группировочного признака;
Xmin – минимальное значение
группировочного признака.
h1=(25286–425)/6 = 4143,5
млн. руб.
Таблица 2 –
Группировка банков по чистым активам, млн. руб.

























№ группы

Группы банков по чистым
активам
Число банков



1

425–4568,5
20


2
4568,5–8712
5


3
8712–12855,5
2


4
12855,5–16999
0


5
16999–21142,5
2


6
21142,5–25286
1


Итого
30



h2 = (1962–5)/6=326,2 млн.
руб.
Таблица 3 – Группировка
банков по прибыли, млн. руб.
























№ группы
Группы банков по прибыли
Число банков


1
5–331,16
24


2
331,16–657,32
4


3
657,32–983,48
1


4
983,48–1309,64
0


5
1309,64–1635,8
0


6
1635,8–1962
1


Итого
30



б) Графики по
данным полученных рядов:
  
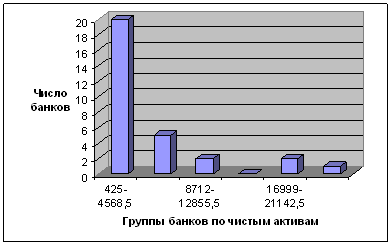
Рисунок 1 – Группировка
банков по чистым активам, млн. руб.
  
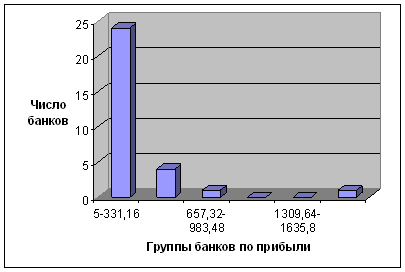
Рисунок 2 – Группировка
банков по прибыли, млн. руб.
в) Средняя
арифметическая взвешенная находится по формуле:
x = ∑ xi * fi / ∑ fi
Таблица 4 –
Таблица для расчета средней арифметической по чистым активам














































№ группы
Группы банков по чистым
активам
Число банков, f

Середина интервала, X i

X*f
S


1
425–4568,5
20
2496,75
49935
20


2
4568,5–8712
5
6640,25
33201,25
25


3
8712–12855,5
2
10783,75
21567,5
27


4
12855,5–16999
0
14927,25
0
27


5
16999–21142,5
2
19070,75
38141,5
29


6
21142,5–25286
1
23214,25
23214,25
30


Итого
30
166059,5



х=166059,5/30=5535,3
млн. руб.
Таблица 5 – Таблица
для расчета средней арифметической по прибыли














































№ группы
Группы банков по
прибыли
Число банков, f

Середина интервала, X i

X* f
S


1
5–331,16
24
168,08
4033,92
24


2
331,16–657,32
4
494,24
1976,96
28


3
657,32–983,48
1
820,4
820,4
29


4
983,48–1309,64
0
1146,56
0
29


5
1309,64–1635,8
0
1472,72
0
29


6
1635,8–1962
1
1798,9
1798,9
30


Итого
30
8630,18



х=8630,18/30=287,7
млн. руб.
Мода
находится по формуле:
Мо = Хо + К*(FMO – FMO — 1 / (FMO – FMO — 1)+(FMO – FMO+1))
где: Хо –
нижняя (начальная) граница модального интервала;
К – величина
интервала;
FMO — частота модального
интервала;
FMO — 1 – частота интервала,
предшествующего модальному;
FMO+1-частота интервала,
следующего за модальным интервалом.
Находим
модальный интервал по наибольшей частоте f1. Наибольшая частота равна
20. Модальный интервал – [425–4568,5]. Хо = 425, К=4143,5
Мо 1
= 425 + 4143,5*(20–0/(20–0)+(20–5))= 2604,04 млн. руб.
Вывод:
наиболее часто встречается банк с размером чистых активов 2604,04 млн. руб.
f2 =24. Модальный интервал –
[5–331,16]. Хо = 5, К=326,2
Мо 2
= 5 + 326,2*(24–0/(24–0)+(24–4))= 178,8 млн. руб.
Вывод:
наиболее часто встречается банк с размером прибыли 178,8 млн. руб.
Для
определения медианы рассчитывают ее порядковый номер (NMe)
NMe = (n+1)/2
NMe = (30+1)/2 = 15,5
Рассчитываем
медиану (Ме) по формуле:
Ме = Хо +
К*((S
f / 2 – SMe — 1) / fMe)
где: Хо –
нижняя граница медианного интервала;
К – величина
интервала;
Sf
= n – число единиц
совокупности;
SMe — 1 – накопленная частота,
предшествующая медианному интервалу;
fMe – медианная частота.
Ме 1
= 425 + 4143,5*((30/2 – 0)/20) = 3426,4 млн. руб.
То есть 15
банков имеет чистые активы более 3426,4 млн. руб. и 15 – менее 3426,4 млн. руб.
Ме 2
= 5 + 326,2*((30/2 – 0)/24) = 207 млн. руб.
То есть 15
банков имеет прибыль более 207 млн. руб. и 15 – менее 207 млн. руб.
Абсолютные
показатели вариации
Размах
вариации – это разность между максимальным и минимальным значением
статистической совокупности. Находится по формуле:
R=Xmax – Xmin
где: Xmax — максимальное значение
признака;
Xmin — минимальное значение
признака.
R1 = 25286–425 = 24861 млн.
руб.
Разница между
банком с максимальным размером чистых активов и банком с минимальным размером
чистых активов равна 24861 млн. руб.
R2 =1962–5 = 1957 млн. руб.
Разница между
банком с максимальным размером прибыли и банком с минимальным размером прибыли
равна 1957 млн. руб.
Среднее
линейное отклонение – это средняя величина из отклонений значений признака от
их средней. Находится по формуле:
d = S
|Xi – X| *fi / S fi
где Xi — значение признака;
Х – среднее
значение признака;
f – частота.
Таблица 6 – Расчет
среднего линейного отклонения по чистым активам














































№ группы
Группы банков по чистым
активам
Число банков, f

Середина интервала, X i


|X i – Х|


|X i – Х|*f



1
425–4568,5
20
2496,75
 — 3038,55
 — 60771


2
4568,5–8712
5
6640,25
1104,95
5524,75


3
8712–12855,5
2
10783,75
5248,45
10496,9


4
12855,5–16999
0
14927,25
9391,95
0


5
16999–21142,5
2
19070,75
13535,45
27070,9


6
21142,5–25286
1
23214,25
17678,95
17678,95


Итого
30
0,5



d = 0,5/30 = 0,02 млн.
руб.
Средняя
величина из отклонений размера чистых активов от их средней составляет 0,02
млн. руб.
Таблица 7 – Расчет
среднего линейного отклонения по прибыли














































№ группы
Группы банков по
прибыли
Число банков, f

Середина интервала, X i


|X i – Х|


|X i – Х|*f



1
5–331,16
24
168,08
 — 119,62
 — 2870,88


2
331,16–657,32
4
494,24
206,54
826,16


3
657,32–983,48
1
820,4
532,7
532,7


4
983,48–1309,64
0
1146,56
858,86
0


5
1309,64–1635,8
0
1472,72
1185,02
0


6
1635,8–1962
1
1798,9
1511,2
1511,2


Итого
30
 — 0,82



d = — 0,82/30 = — 0,03 млн.
руб.
Средняя
величина из отклонений размера прибыли от их средней составляет — 0,03 млн. руб.
Дисперсия –
средний квадрат отклонений индивидуальных значений признака от их средней
величины. Находится по формуле:
s
2 = S (Xi – X)2 *fi / S fi
Таблица 8 – Расчет
дисперсии по чистым активам














































Группы банков по чистым
активам
Число банков, f

Середина интервала, X i


X i – Х


(X i – Х)2


(X i – Х)
2 *f




425–4568,5

20
2496,75
 — 3038,55
9232786,1
184655722


4568,5–8712
5
6640,25
1104,95
1220914,5
6104572,5


8712–12855,5
2
10783,75
5248,45
27546227,4
55092454,8


12855,5–16999
0
14927,25
9391,95
88208724,8
0


16999–21142,5
2
19070,75
13535,45
183208406,7
366416813,4


21142,5–25286
1
23214,25
17678,95
312545273,1
312545273,1


Итого
30
924814835,8



s
2 =924814835,8/30=30827161,2 млн. руб.
Таблица 9 – Расчет
дисперсии по прибыли














































Группы банков по прибыли
Число банков, f

Середина интервала, X i


X i – Х


(X i – Х)2


(X i – Х)
2 *f



5–331,16
24
168,08
 — 119,62
14308,9
343414,7


331,16–657,32
4
494,24
206,54
42658,8
170635,1


657,32–983,48
1
820,4
532,7
283769,3
283769,3


983,48–1309,64
0
1146,56
858,86
737640,5
0


1309,64–1635,8
0
1472,72
1185,02
1404272,4
0


1635,8–1962
1
1798,9
1511,2
2283725,4
2283725,4


Итого
30
3081544,5



s
2 = 3081544,5 /30 =102718,1 млн. руб.
Среднее
квадратическое отклонение – это корень квадратный из дисперсии. Находится по
формуле:
σ= Ö (S (Xi – X)2*fi /S fi)
σ= Ö 30827161,2 =5552,2 млн.
руб.
σ= Ö 102718,1 = 320,5 млн.
руб.
Относительные
показатели вариации
В общем виде
они показывают отношение абсолютных показателей вариации к средней величине. К
ним относятся:
Коэффициент
осцилляции. Находится по формуле:
VR = R / x * 100%
VR1 = 24861 / 5535,3 * 100% =
449,1%
VR2 =1957 / 287,7 *100% = 680,2%
Относительное
линейное отклонение. Находится по формуле:
Vd = d / x * 100%
Vd1 = 0,02 / 5535,3 * 100% =
0,0004%
Vd1 = — 0,03 / 287,7* 100% = — 0,01%
Коэффициент
вариации (характеризует однородность совокупности). Находится по формуле:
Vσ = σ / x * 100%
Vσ1= 5552,2 / 5535,3 * 100%
= 100% > 33% (совокупность неоднородная)
V σ1= 320,5/ 287,7* 100% = 111%>
33% (совокупность неоднородная)
г)
Определение количественных характеристик распределения. К ним относятся:
– Показатель
асимметрии. Находится по формуле:
As = m3 / s 3
m3 = S (Xi – X)3 * fi / S fi
где: m3 – центральный момент 3 – го порядка;
s
3 — среднее квадратичное отклонение в кубе.
Таблица 10 – Расчет
асимметрии по чистым активам, млн. руб.














































Группы банков по чистым
активам
Число банков, f

Середина интервала, X i


X i – Х


(X i – Х)3


(X i – Х)
3 *f



425–4568,5
20
2496,75
 — 3038,55
 — 28054282211,7
 — 561085644234


4568,5–8712
5
6640,25
1104,95
134909479,5
674547397,5


8712–12855,5
2
10783,75
5248,45
144574997210,6
289149994421,2


12855,5–16999
0
14927,25
9391,95
828451932908,8
0


16999–21142,5
2
19070,75
13535,45
2479808228501,3
4959616457002,6


21142,5–25286
1
23214,25
17678,95
5525472255915,4
5525472255915,4


Итого
30
10213827610502,7



m3 =10213827610502,7 / 30 = 340460920350,1
As = 340460920350,1/171157252096,6
= 1,9 > 0, асимметрия правосторонняя
Таблица 11 – Расчет
асимметрии по прибыли, млн. руб.














































Группы банков по прибыли
Число банков, f

Середина интервала, X i


X i – Х


(X i – Х)3


(X i – Х)
3 *f



5–331,16
24
168,08
 — 119,62
 — 1711635,9
 — 41079261,6


331,16–657,32
4
494,24
206,54
8810742,7
35242970,8


657,32–983,48
1
820,4
532,7
151163900,8
151163900,8


983,48–1309,64
0
1146,56
858,86
633529919,5
0


1309,64–1635,8
0
1472,72
1185,02
1664090879,9
0


1635,8–1962
1
1798,9
1511,2
3451165884,9
3451165884,9


Итого
30
3596493494,9



m3 = 3596493494,9 / 30 = 119883116,5
As = 119883116,5/32921840,1=
3,6>0, асимметрия является правосторонней.
Чтобы
определить является ли асимметрия существенной или несущественной рассчитывают
отношение показателя асимметрии к среднеквадратическому отклонению:
As / sAs
где: sAs — среднеквадратическая
ошибка асимметрии.
Она зависит
от объема совокупности и рассчитывается по формуле:
sAs = Ö 6*(n – 1)/(n+1)*(n+3)
sAs = Ö 6 * (30 – 1)/(30+1)*(30+3)
= 0,4
As
/ sAs (по чистым активам) = 1,9 / 0,4
= 4,75>3
As / sAs (по прибыли) = 3,6/ 0,4 =
9>3
Таким
образом, As / sAs во всех случаях > 3 Þ асимметрия существенна. Так
как асимметрия существенна, эксцесс не рассчитывается.
д) Нахождение
эмпирической функции и построение ее графика.
Для удобства
вычислений вероятностей случайные величины нормируются, а затем по специальным
таблицам находим плотность распределения нормированной случайной величины:
t = (xi – x) / s
f | = (S f * k / s)* j (t)
Таблица 14 – Расчет
теоретических частот по чистым активам















































Середина интервала, X i

Число банков, f

X i – Х

t
j (t)

f |




2496,75

20
 — 3038,55
 — 0,54
0,3448
8,0


6640,25
5
1104,95
0,19
0,3918
9,0


10783,75
2
5248,45
0,94
0,2565
6,0


14927,25
0
9391,95
1,69
0,0957
2,0


19070,75
2
13535,45
2,44
0,0203
0


23214,25
1
17678,95
3,18
0,0025
0


Итого
30
25



Таблица 15 – Расчет
теоретических частот по прибыли















































Середина интервала, X i

Число банков, f

X i – Х

t
j (t)

f |




168,08

24
 — 119,62
 — 0,37
0,3726
11,0


494,24
4
206,54
0,64
0,3251
10,0


820,4
1
532,7
1,66
0,1006
3,0


1146,56
0
858,86
2,68
0,0110
0


1472,72
0
1185,02
3,69
0,0004
0


1798,9
1
1511,2
4,71
—
0


Итого
30
24



  
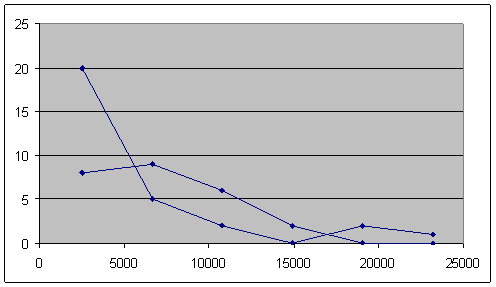
Рисунок 3 –
Эмпирическая и теоретическая функции распределения по чистым активам
  
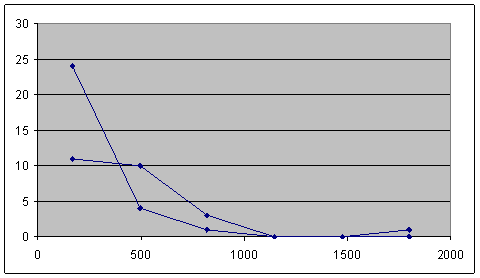
Рисунок 4 – Эмпирическая
и теоретическая функции распределения по прибыли
ж) Проверим
гипотезу о том, что изучаемые признаки подчиняются нормальному закону
распределения с помощью математического критерия Романовского:
r
=(c2расч — (h-l‑1))/Ö2 – (h-l‑1)
c2расч = S(f – f |)2 / f
где: f – эмпирические частоты;
f | – теоретические частоты.
h – число групп;
l – число независимых
параметров, которые необходимо знать, чтобы построить кривую теоретического
распределения.
Таблица 16 –
Проверка гипотезы по размеру чистых активов















































Группы банков по чистым
активам
Число банков, f

f |


(f- f |)


(f- f |)2


(f- f |)2/f



425–4568,5
20
8,0
12,0
1440
7,2


4568,5–8712
5
9,0
 — 4,0
16,0
3,2


8712–12855,5
2
6,0
 — 4,0
16,0
8,0


12855,5–16999
0
2,0
 — 2,0
4,0
0,0


16999–21142,5
2
0
2,0
4,0
2,0


21142,5–25286
1
0
1,0
1,0
1,0


Итого
30
25
22,4



c2расч = 22,4
r
= (22,4 – (6–2–1))/Ö(2*(6–2–1))= 7,9>3, следовательно, что
гипотеза о соответствии распределения банков по размеру чистых активов закону
нормального распределения отвергается
Таблица 17 – Проверка
гипотезы по размеру прибыли















































Группы банков по
прибыли
Число банков, f

f |


(f- f |)


(f- f |)2


(f- f |)2/f



5–331,16
24
11,0
13,0
169,0
7,0


331,16–657,32
4
10,0
 — 6,0
36,0
9,0


657,32–983,48
1
3,0
 — 2,0
4,0
4,0


983,48–1309,64
0
0
0
0
0


1309,64–1635,8
0
0
0
0
0


1635,8–1962
1
0
1,0
1,0
1,0


Итого
30
24
21



c2расч = 21
r
= (21 – (6–2–1))/Ö(2*(6–2–1))= 7,3 > 3, следовательно, что
гипотеза о соответствии распределения банков по размеру прибыли закону нормального
распределения отвергается.
з)
Определение границ, в которых с вероятностью 0,95 будет находиться среднее
значение выбранных показателей в генеральной совокупности. Средняя ошибка
выборки определяется по формуле:
m
= Ös2 / n * (1 – (n/N))
где: n – число единиц в
выборочной совокупности;
N – число единиц в
генеральной совокупности.
m 
= Ö 30827161,2 /30*(1 – (30/200))=
1099,5 млн. руб.
m 
= Ö102718,1 /30*(1 – (30/200))=63,5
млн. руб.
Предельная
ошибка выборки определяется по формуле:
D
= m
* t
где t – коэффициент доверия,
определяемый в зависимости от вероятности по таблицам. p = 0,95 Þ t = 1,96
D
= 1099,5*1,96 = 2155,02 млн. руб.
D
= 63,5*1,96 = 124,4 млн. руб.
Границы
среднего значения показателя определяются по формуле:
Х= Х ± D
где: Х –
среднее арифметическое значение признака.
Х = 5535,3+ 2155,02
=7690,3 млн. руб.
Х = 5535,3 –
2155,02 =3380,5 млн. руб.
Х = 287,7 +124,4=
412,1 млн. руб.
Х = 287,7 – 124,4=
163,3 млн. руб.
Границы, в
которых с вероятностью 0,95 будет находиться среднее значение показателя чистых
активов в генеральной совокупности, лежит в пределах 3380,5 млн. руб. < Х < 7690,3 млн. руб.
Границы, в
которых с вероятностью 0,95 будет находиться среднее значение показателя
прибыль в генеральной совокупности, лежит в пределах 163,3 млн. руб.< Х < 412,1 млн. руб.
По выше
приведенным расчетам можно сделать следующие выводы:
– из 30
отобранных банков, наиболее часто встречаются банки с размером чистых активов 2604,04
млн. руб., с размером прибыли 178,8 млн. руб.;
– из
отобранных банков 15 имеют размер чистых активов больше 3426,4 млн. руб. и 15
менее. И прибыль 15 банков больше 207 млн. руб., а у 15 менее;
– по
данным абсолютных показателей вариации выборки по прибыли значительно ниже, чем
по чистым активам;
– по
данным относительных показателей совокупность неоднородная. Ассиметрия по
чистым активам и по прибыли является правосторонней.
– границы,
в которых с вероятностью 0,95 будет находиться среднее значение показателя
чистых активов в генеральной совокупности, лежит в пределах
3380,5 млн.
руб. < Х < 7690,3 млн. руб., прибыль в пределах 163,3 млн.
руб.< Х < 412,1 млн. руб.;
– гипотеза
о том, что изучаемые признаки подчиняются нормальному закону распределения
отвергается;
– зависимость
между чистыми активами и прибылью по тесноте связи сильная, по направлению
прямая;
– параметр
коэффициента а не значим и не может распространяться на всю совокупность, а
параметр b
значим и его можно разместить на всю совокупность;
– коэффициент
корреляции статистически значим.
Список
используемой литературы
1. Конспект лекций
2. Статистика: учеб./ И.И. Елисеева А.В.