Статистичні коефіцієнти рентабельності роботи комерційних банків
МІНІСТЕРСТВО
ОСВІТИ УКРАЇНИНАЦІОНАЛЬНИЙ
ГІРНИЧИЙ УНІВЕРСИТЕТКафедра
менеджментуКУРСОВИЙ ПРОЕКТ
з дисципліни “Статистика”
Виконала
студентка ІІІ курс, з/в
групи Ф — 99
Шибка Т.В.
варіант №17
Перевірив: доц. Барабан О.А.
Дніпропетровськ
Зміст
Вступ………………………………………………………………………………………………………………..3
Вихідні індивідуальні данні варіанту №17…………………………………………………………7
І.
Зведення та групування статистичних даних за факторною
ознакою……………….9
ІІ. Зведення і групування
статистичних даних за результативною ознакою………..13
ІІІ. Обчислення показників
варіації…………………………………………………………………..16ІV. Статистичні методи вивчення взаємозв’язків між факторною та
резуль-тативною
ознаками…………………………………………………………………………………………..18V.
Обчислення характеристик рядів
динаміки…………………………………………………..23VI. Розрахунок
індексів…………………………………………………………………………………….36Висновки…………………………………………………………………………………………………………39
Перелік
використаної
літератури………………………………………………………………………40
ВСТУП
Статистика
вивчає розміри і кількісні співвідношення масових суспільно-економічних явищ і
процесів у нерозривному зв’язку з їх якісним змістом. Для того, щоб виявити та
охарактеризувати розміри, їх зміни і кількісні співвідношення конкретних
масових суспільних явищ, необхідно послідовно здійснити такі три основі стадії
економіко-статистичного дослідження: 1) статистичне спостереження; 2)
статистичне зведення і групування первинних даних; 3) аналіз статистичної
інформації. Для вивчення кількісного аспекту масових суспільно-економічних явищ
і процесів статистика використовує ряд понять і категорій: ознака, варіація,
статистична сукупність, показник, система показників. Статистична сукупність –
це велика кількість одиниць, об’єктів, явищ, об’єднаних будь-якими загальними
властивостями (ознаками), що піддаються статистичному вивченню
Закон
великих чисел – це один із основних законів який використовується статистикою
для дослідження явищ суспільного життя. Він дає змогу зрозуміти, чому із
великої кількості хаосу випадкових зв’язків ми можемо встановити і встановлюємо
закономірності у розвитку суспільних явищ. Кожне окреме явище суспільного життя
завжди унікальне, тому що на нього впливає велика кількість випадкових
чинників. Розпізнати між ними закономірність у кожному конкретному випадку
практично неможливо. Але якщо вивчати ці явища у значній кількості, то можна
з’ясувати закономірності, оскільки випадкові відхилення, властиві кожному
окремому явищу, в своїй сукупності нейтралізують одне одного.
Закономірність
– це повторюваність, послідовність та порядок у розвитку соціальних явищ. Вона
може проявлятися по-різному. В філософії розрізняють два види закономірностей:
динамічну та статистичну.
Динамічна
закономірність – це така, яка виявляється в кожному окремому випадку і
не залежить від кількості одиниць, які ми спостерігаємо. Вона притаманна
природним явищам. Наприклад, закон Архімеда можна виявити і в одному об’єкті,
який занурюють в рідину, і на тисячі об’єктів. Статистична
закономірність – це така, яка виявляється лише в достатній кількості
однорідних одиничних елементів, котрі й утворюють сукупність. Тобто кожний
окремий елемент може не підтверджувати існування тієї чи іншої закономірності,
тому що існування її в кожному окремому елементі носить імовірний характер.
Інакше кажучи, статистична закономірність властива лише сукупності одиниць, яка
має назву статистичної сукупності.
Статистичні
закономірності проявляються по-різному. Це можуть бути закономірності: 1)
розвитку (динаміки) явищ (статистика свідчить про збільшення чисельності
населення, зростання тривалості життя, зменшення середнього віку обрання
шлюбу); 2) структурних зрушень (збільшення частки міського населення в
загальній його чисельності, а також частки населення похилого віку в сільській
місцевості); 3) розподілу елементів сукупності (розподіл населення за віком,
сімей за числом дітей, середньодушовим доходом); 4) зв’язку між явищами
(залежність прибутку від фондоозброєності, собівартості продукції,
продуктивності праці).
Статистична
сукупність – це певна множина елементів, поєднаних однаковими умовами
існування та розвитку. Об’єктивною основою існування статистичної сукупності є
складне перетинання причин та умов, які формують той чи інший масовий процес,
наприклад, зміни тенденції в розвитку злочинності від зміни
соціально-економічної та політичної ситуації в країні.
Кожний
окремий елемент, який складає статистичну сукупність, має назву одиниці
сукупності. Кожна окрема одиниця сукупності є носієм явища, що вивчається,
і відрізняється від іншої одиниці сукупності розміром ознаки. Завжди має місце
коливання (варіювання) значень ознаки у кожній одиниці статистичної сукупності.
Явищами
хімії, фізики, математики та інших природничих наук властиві лише динамічні
закономірності.
Явища
суспільного життя, які вивчаються статистикою, відносяться до статистичних
закономірностей. Окремі елементи статистичної сукупності характеризуються
значною кількістю різних ознак, але відповідно до мети дослідження вони мають
загальні властивості, що і робить їх статистичною сукупністю. Ознака, яка
приймає в межах сукупності різні значення , називається варіюючою, а
відмінність, коливання значень ознаки – варіацією. Склад елементів і спосіб
об’єднання їх визначають структуру сукупності.
Ознаки
поділяються на кількісні і атрибутивні (словесні). Якщо кількісна ознака
представлена числом (стаж роботи, заробітна плата), то застосовують загально
визнані еталони і одиниці виміру. Для атрибутивних ознак вимірювання означає
реєстрацію наявності чи відсутності властивості, що вивчається (категорійні
підрахунки).
Набір
властивостей явища і відповідних їм чисел називають шкалою вимірювання.
Теоретично існує багато типів шкал. За рівнем вимірювання і допустимими
арифметичними діями виділяють метричну, номінальну, порядкову (рангову) шкали.
Метрична
– це звичайна числова шкала обчислення, яку використовують для вимірювання
фізичних величин ваги, довжини, часу) або результатів обчислення (прибуток,
середня заробітна плата). Ознаки метричної шкали поділяються на дискретні і
неперервні. Дискретні мають лише окремі, ізольовані значення. Найчастіше це
результати лічби. Неперервні ознаки мають будь-які значення в певних межах.
Така визначеність неперервної ознаки дещо умовна, її завжди можна представити
дискретною.
Номінальна
– це шкала найменувань. “Оцифровка” ознак цієї шкали проводиться таким
чином, щоб подібним елементам відповідало одне й те саме число, а неподібним –
різні числа. Найчастіше використовують штучні вимірники, які приймають значення
“1” або “0” залежно від наявності чи відсутності властивості, що вивчається.
Порядкова
(рангова) шкала встановлює не тільки відношення подібності елементів, а й послідовності
– порядку. Це відношення типу “більше, ніж”, “краще, ніж” тощо. Кожному пункту
шкали приписується число – ранг, число балів або будь-яка монотонно зростаюча
функція ( — 2, — 1, 0, 1, 2), що відбиває послідовність значень, але не відстань
між ними.
Математично
вивчати статистичну закономірність дає змогу використання тільки закону великих
чисел. Закон великих чисел – це математично обґрунтована теорія,
відповідно до якої, спираючись на знання теорії ймовірностей, можна
стверджувати, що спільна дія значної кількості випадкових фактів призводить до
наслідків, які не залежать від випадку. Проте закон великих чисел не може
визначити ні рівень, ні динаміку розвитку суспільного явища. Він лише обумовлює
взаємо погашення випадкових відхилень, які властиві окремим одиницям
статистичної сукупності, дозволяє виявити в ній дію об’єктивних законів
розвитку суспільних явищ.
В
даній курсовій роботі на базі статистичного аналізу первинних даних рядів
динаміки показників ресурсів(активів) 60 комерційних банків та ефективності
роботи цих активів, виражених в зароблених сумах прибутку банку, проведено
аналітично-розрахункове дослідження центральних тенденцій рядів розподілів та
їх характеристика середніми величинами, базовими та цепними індексами і темпами
росту , агрегатними індексами та темпами росту агрегатних комплексів. На основі
регресійного аналізу взаємозв ‘ язку середніх величин факторних величин
(активів) та результатних величин (прибутку) розраховані статистичні
коефіцієнти рентабельності роботи комерційних банків у приведеній статистичній
виборці.
Вихідні
індивідуальні данні
В табл.1 наведені розраховані згідно методичних
вказівок вихідні дані для індивідуального номеру в журналі групи № 17 та номеру
групи 1 (для варіантів колонок ОА — 97 № 1)
Таблиця
1.
Вихідні
дані (варіант 17)
| № п/п | Активи, млн.грн. | Прибуток, млн.грн. | |||||||
| 1999 | 2000 | 1999 | 2000 | ||||||
| з табл. 1 | з табл. 1 |
розрахун-кові | з табл. 1 | розрахун-кові | з табл. 1 | розрахун-кові | з табл. 1 | розрахун-кові | |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 17 | 1 | 31,3 | 35,3 | 32,6 | 36,6 | 5 | 7 | 5,2 | 7,2 |
| 18 | 2 | 60,2 | 60,2 | 60,3 | 60,3 | 2,5 | 2,5 | 2,4 | 2,4 |
| 19 | 3 | 19,6 | 23,6 | 21,2 | 25,2 | 4,2 | 6,2 | 4,3 | 6,3 |
| 20 | 4 | 45,5 | 45,5 | 47,4 | 47,4 | 5 | 5 | 5,1 | 5,1 |
| 21 | 5 | 60 | 64 | 57 | 61 | 2,1 | 4,1 | 2,3 | 4,3 |
| 22 | 6 | 37,8 | 37,8 | 38,6 | 38,6 | 1,8 | 1,8 | 2,1 | 2,1 |
| 23 | 7 | 30,1 | 34,1 | 32 | 36 | 4,2 | 6,2 | 4,4 | 6,4 |
| 24 | 8 | 28,4 | 28,4 | 30,7 | 30,7 | 1 | 1 | 1,1 | 1,1 |
| 25 | 9 | 60,1 | 64,1 | 60,6 | 64,6 | 3,5 | 5,5 | 3,7 | 5,7 |
| 26 | 10 | 35 | 35 | 35,1 | 35,1 | 1,7 | 1,7 | 2,2 | 2,2 |
| 27 | 11 | 24,9 | 28,9 | 26,7 | 30,7 | 0,6 | 2,6 | 0,5 | 2,5 |
| 28 | 12 | 20,3 | 20,3 | 21,3 | 21,3 | 2,1 | 2,1 | 2,3 | 2,3 |
| 29 | 13 | 34,4 | 38,4 | 36 | 40 | 2 | 4 | 2,2 | 4,2 |
| 30 | 14 | 38,2 | 38,2 | 38,7 | 38,7 | 3,9 | 3,9 | 3,7 | 3,7 |
| 31 | 15 | 9,8 | 13,8 | 10,1 | 14,1 | 0,7 | 2,7 | 0,8 | 2,8 |
| 32 | 16 | 21,4 | 21,4 | 22,3 | 22,3 | 1 | 1 | 1,2 | 1,2 |
| 33 | 17 | 18,3 | 22,3 | 19,5 | 23,5 | 3,1 | 5,1 | 3 | 5 |
| 34 | 18 | 16,2 | 16,2 | 16,4 | 16,4 | 1,3 | 1,3 | 1,1 | 1,1 |
| 35 | 19 | 16,5 | 20,5 | 16,6 | 20,6 | 0,5 | 2,5 | 0,6 | 2,6 |
| 36 | 20 | 7,6 | 7,6 | 7,5 | 7,5 | 0,6 | 0,6 | 0,7 | 0,7 |
| 37 | 21 | 17,1 | 21,1 | 17,4 | 21,4 | 3,5 | 5,5 | 3,6 | 5,6 |
| 38 | 22 | 11,6 | 11,6 | 12,2 | 12,2 | 1,7 | 1,7 | 1,9 | 1,9 |
| 39 | 23 | 17,5 | 21,5 | 18 | 22 | 0,8 | 2,8 | 0,9 | 2,9 |
| 40 | 24 | 9 | 9 | 9,3 | 9,3 | 0,2 | 0,2 | 0,3 | 0,3 |
| 41 | 25 | 17,2 | 21,2 | 18,4 | 22,4 | 0,6 | 2,6 | 0,6 | 2,6 |
| 42 | 26 | 34,4 | 34,4 | 34,5 | 34,5 | 3,4 | 3,4 | 3,5 | 3,5 |
| 43 | 27 | 9,2 | 13,2 | 9,4 | 13,4 | 0,3 | 2,3 | 0,2 | 2,2 |
| 44 | 28 | 8,9 | 8,9 | 10,2 | 10,2 | 1,4 | 1,4 | 1,5 | 1,5 |
| 45 | 29 | 8,8 | 12,8 | 9,9 | 13,9 | 0,3 | 2,3 | 0,5 | 2,5 |
| 46 | 30 | 25,1 | 25,1 | 26 | 26 | 1,8 | 1,8 | 2 | 2 |
| 47 | 31 | 27,6 | 31,6 | 27,8 | 31,8 | 1,4 | 3,4 | 1,6 | 3,6 |
| 48 | 32 | 18,7 | 18,7 | 19,1 | 19,1 | 1,1 | 1,1 | 1,4 | 1,4 |
| 49 | 33 | 11,7 | 15,7 | 12,7 | 16,7 | 1,6 | 3,6 | 1,9 | 3,9 |
| 50 | 34 | 9,2 | 9,2 | 10,4 | 10,4 | 1,4 | 1,4 | 1,5 | 1,5 |
| Продовження табл.1 | |||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 51 | 35 | 37,3 | 41,3 | 38 | 42 | 1,7 | 3,7 | 1,8 | 3,8 |
| 52 | 36 | 6,8 | 6,8 | 6,8 | 6,8 | 0,6 | 0,6 | 0,9 | 0,9 |
| 53 | 37 | 6,8 | 10,8 | 6,9 | 10,9 | 1,1 | 3,1 | 1,4 | 3,4 |
| 54 | 38 | 7,5 | 7,5 | 8 | 8 | 0,5 | 0,5 | 0,4 | 0,4 |
| 55 | 39 | 10,1 | 14,1 | 10,3 | 14,3 | 1,6 | 3,6 | 1,7 | 3,7 |
| 56 | 40 | 19,9 | 19,9 | 20,8 | 20,8 | 0,6 | 0,6 | 0,9 | 0,9 |
| 57 | 41 | 8,1 | 12,1 | 8,5 | 12,5 | 0,5 | 2,5 | 0,3 | 2,3 |
| 58 | 42 | 10,2 | 10,2 | 10,5 | 10,5 | 0,9 | 0,9 | 1 | 1 |
| 59 | 43 | 8,3 | 12,3 | 8,5 | 12,5 | 1,1 | 3,1 | 1,3 | 3,3 |
| 60 | 44 | 4,7 | 4,7 | 4,5 | 4,5 | 0,4 | 0,4 | 0,4 | 0,4 |
| 61 | 45 | 14,9 | 18,9 | 15 | 19 | 0,2 | 2,2 | 0 | 2 |
| 62 | 46 | 9,5 | 9,5 | 9,2 | 9,2 | 1 | 1 | 1,2 | 1,2 |
| 63 | 47 | 4,4 | 8,4 | 4,3 | 8,3 | 0,1 | 2,1 | 0 | 2 |
| 64 | 48 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 |
| 65 | 49 | 6,5 | 10,5 | 6,7 | 10,7 | 1,8 | 3,8 | 2 | 4 |
| 66 | 50 | 5,8 | 5,8 | 5,7 | 5,7 | 0,1 | 0,1 | 0,2 | 0,2 |
| 67 | 51 | 7,7 | 11,7 | 7,9 | 11,9 | 0,1 | 2,1 | 0,3 | 2,3 |
| 68 | 52 | 8,7 | 8,7 | 9 | 9 | 0,3 | 0,3 | 0,4 | 0,4 |
| 69 | 53 | 6,2 | 10,2 | 6,4 | 10,4 | 0,1 | 2,1 | 0,1 | 2,1 |
| 70 | 54 | 10 | 10 | 10,8 | 10,8 | 0,7 | 0,7 | 0,9 | 0,9 |
| 71 | 55 | 8 | 12 | 8,2 | 12,2 | 0,4 | 2,4 | 0,7 | 2,7 |
| 72 | 56 | 5 | 5 | 5,2 | 5,2 | 0,7 | 0,7 | 0,6 | 0,6 |
| 73 | 57 | 7 | 11 | 7,2 | 11,2 | 0,2 | 2,2 | 0,3 | 2,3 |
| 74 | 58 | 9,6 | 9,6 | 9,8 | 9,8 | 0,2 | 0,2 | 0,3 | 0,3 |
| 75 | 59 | 5,5 | 9,5 | 5,8 | 9,8 | 1,5 | 3,5 | 1,4 | 3,4 |
| 76 | 60 | 5 | 5 | 5,2 | 5,2 | 0,6 | 0,6 | 0,5 | 0,5 |
В табл. 1 в графі
“розрахункові” дані отримані наступним чином:
активи: кожне
непарне (1,3,5,…,59) значення + (номер групи*4) = кожне непарне значення +
1*4;
прибуток: кожне
непарне (1,3,5,…,59) значення + (номер групи*2) = кожне непарне значення +
1*2.
В табл.2 вихідних даних приведені
розраховані згідно алгоритму методичних вказівок щомісячні показники вартості
активів по банку № 17 (варіант завдання ) за 1996 –2000 роки.
Таблиця
2.
Вартість
активів за роками по 17-ому банку
| Місяць | Вартість активів за роками, млн.грн. | ||||
| 1996 | 1997 | 1998 | 1999 | 2000 | |
| 1 | 36,89 | 27,96 | 30,52 | 37,07 | 37,33 |
| 2 | 32,86 | 29,85 | 29,87 | 36,36 | 36,97 |
| 3 | 31,86 | 30,79 | 30,84 | 35,65 | 35,50 |
| 4 | 31,52 | 30,16 | 30,20 | 36,01 | 35,87 |
| 5 | 30,52 | 30,47 | 31,48 | 34,95 | 35,14 |
| 6 | 30,18 | 31,10 | 33,73 | 33,54 | 33,31 |
| 7 | 29,51 | 31,73 | 34,69 | 34,59 | 32,57 |
| 8 | 29,85 | 32,05 | 32,77 | 33,89 | 32,21 |
| 9 | 31,52 | 32,99 | 32,44 | 34,59 | 31,84 |
| 10 | 30,52 | 31,10 | 31,80 | 34,95 | 32,57 |
| 11 | 30,85 | 30,79 | 35,34 | 36,01 | 31,84 |
| 12 | 33,54 | 31,42 | 32,12 | 35,30 | 36,60 |
І. Зведення та групування статистичних даних за факторною
ознакою
Завдання
етапу І :
Вихідні
дані 2000 р. (табл. 1) проранжирувати, вибрати факторну ознаку і за нею
побудувати ряд розподілу, утворивши 5 груп з рівними інтервалами. Резуль-тати
побудови ряду розподілу оформити у вигляді таблиці. Побудований ряд розподілу
зобразити графічно на основі звичайних і кумулятивних частот.
За
роллю, яку відіграють ознаки у взаємозв’язку досліджуваних явищ, їх поділяють
на факторні, що впливають на інші ознаки, і результативні, розмір
і динаміка яких формуються під впливом інших ознак.
Обираємо
факторну ознаку – активи. Групування виконується при рівних
інтервалах та числі груп 4. Розмір інтервалу визначається за формулою:
![]()
Розмір інтервалу приймається рівним 15,4
млн.грн.. Розраховуємо та побудуємо табл.3
Таблиця 3
Обчислення
характеристик центра розподілу
| Групи одиниць сукупності за результативною ознакою |
Кількість одиниць (частота), f |
Середина |
Варіанти зважені |
Кумулятивні частоти, S |
| 3–18,4 | 33 | 10,7 | 353,1 | 33 |
| 18,4–33,8 | 15 | 26,1 | 391,5 | 48 |
| 33,8–49,2 | 9 | 41,5 | 373,5 | 57 |
| 49,2–64,6 | 3 | 56,9 | 170,7 | 60 |
| Всього | 60 | – | 1288,8 | – |
Для інтервального варіаційного ряду порядок розрахунку моди
та медіани наступний: спочатку находять інтервал, якому належить мода чи
медіана, а потім розраховують відповідні значення цих показників.
Модальним
в даному розподілі є інтервал 3-18,4, так як найбільше число банків f=33
находиться в цьому інтервалі. Значення моди визначається за формулою:
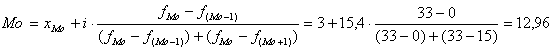 млн. грн.
млн. грн.
де і –величина
інтервалу; fMo – частота модального інтервалу; fMo — 1 –
частота інтервалу, що передує модальному; fMo+1 – частота
інтервалу, наступного за модальним.
Моду
можна визначити за гістограмою розподілу.
Гістограма
– це графічне зображення інтервального варіаційного ряду. На осі абсцис
відкладають розміри ознак (варіанти). Утворені прямокутники пропор-ційні за
висотою частотам значень ознаки по кожному інтервалу[5].
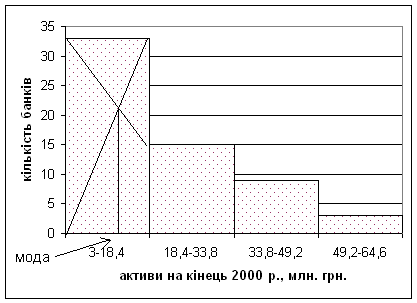
Рис. 1. Гістограма розподілу активів на кінець
2000 р.
Медіана
відповідає варіанту, що стоїть в середині ранжированого ряду. Положення медіани
визначається її номером:
Місце
медіани ![]() , де n — число одиниць
, де n — число одиниць
сукупності.
Медіанним
є інтервал 3-18,4, так як в цьому інтервалі находяться номери 30 і 31 ряду.
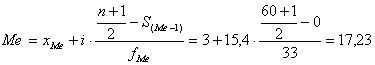 млн. грн.
млн. грн.
де xMe –
нижня границя медіанного інтервалу; і – величина інтервалу; S(Me — 1)
– накопичена частота інтервалу, що передує медіанному; f – частота медіанного
інтервалу.
Медіана
визначається по кумуляті. Для її визначення висоту найбільшої ординати, котра
відповідає загальній кількості, ділять пополам. Через отриману точку проводять
пряму, паралельно вісі абсцис, до перетину її з кумулятою. Абсциса точки
перетину є медіанною величиною[1].
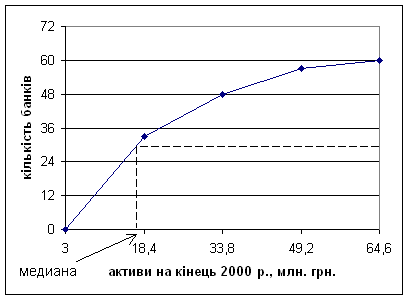
Рис. 2. Кумулятивна крива розподілу активів на кінець 2000 р.
Середня величина активів на кінець 2000 року
дорівнює
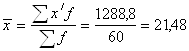 млн. грн.
млн. грн.
Висновки І. Вибірка факторної ознаки – активів банків має характеристики:
Мода
– це величина, яка найчастіше зустрічається в даній сукупності. У варіаційному
ряді це буде варіант, що має найбільшу частоту.
Мода
активів досліджуємої вибірки банків= 12,96 млн. грн.
Медіана
– це варіант, що знаходиться в середині упорядкованого варіаційного ряду, тобто
ділить його на дві рівні частини. Медіана показує величину варіюючої ознаки,
якої досягла половина сукупності.
Медіана
активів досліджуємої вибірки банків = 17,23 млн. грн.
Середня
величина це показник, що характеризує типовий рівень варіюючої ознаки в
розрахунку на одиницю однорідної сукупності.
Середня
величина активів розрахована за формулою середньої зваженої і дорівнює = 21,48
млн. грн.
Різниця між
середньою величиною та характеристиками моди і медіани вибірки факторної
ознаки свідчить про наявність суттєвих нерівномірностей кількісного розподілу
банків по гістограмам факторних та результативних ознак,
тобто середня величина для даної виборки є
недостатньо характерна величина.
ІІ. Зведення і
групування статистичних даних за результативною ознакою
Завдання
етапу 2.
За
вихідними даними 2000 р. (табл. 1) побудувати ряд розподілу за резуль-тативною
ознакою, утворивши 4 групи з рівними інтервалами. На його основі обчислити
характеристики розподілу – середню величину, моду і медіану (аналі-тично і
графічно). Методику обчислення середньої величини та необхідних величин для
розрахунку показати в таблиці.
Обираємо результативну
ознаку – прибуток. Групування виконується при рівних інтервалах та числі
груп 4. Розмір інтервалу визначається за формулою[3]:
![]()
Розмір інтервалу приймається рівним 1,75
млн.грн.. Розраховуємо та побудуємо табл.4
Таблиця 4
Обчислення характеристик центра розподілу
| Групи одиниць сукупності за результативною ознакою |
Кількість одиниць (частота), f |
Середина |
Варіанти зважені |
Кумулятивні частоти, S |
| 0,2 – 1,95 | 21 | 1,075 | 22,575 | 21 |
| 1,95 – 3,7 | 26 | 2,825 | 73,45 | 47 |
| 3,7 – 5,45 | 8 | 4,575 | 36,6 | 55 |
| 5,45 – 7,2 | 5 | 6,325 | 31,625 | 60 |
| Всього | 60 | – | 164,25 | – |
Модальним в даному
розподілі є інтервал 1,95–3,7, так як найбільше число банків f=26
находиться в цьому інтервалі. Значення моди визначається за формулою:
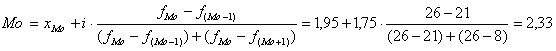 млн. грн.
млн. грн.
де і –величина
інтервалу; fMo – частота модального інтервалу; fMo — 1 –
частота інтервалу, що передує модальному; fMo+1 – частота
інтервалу, наступного за модальним.
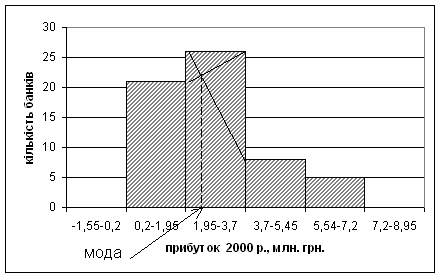
Рис. 3. Гістограма розподілу прибутку 2000 р.
по 60 банках.
Місце
медіани ![]() , де n — число одиниць
, де n — число одиниць
сукупності.
Медіанним є інтервал 1,95–3,7, так як
в цьому інтервалі находяться номери 30 і 31 ряду.
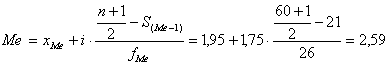 млн. грн.
млн. грн.
де xMe – нижня границя медіанного
інтервалу; і – величина інтервалу; S(Me — 1) – накопичена частота
інтервалу, що передує медіанному; f – частота медіанного інтервалу.
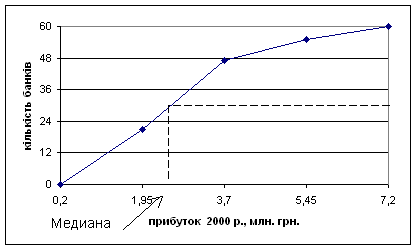
Рис. 4. Кумулятивна крива розподілу прибутку 2000 р. по 60 банках.
Середня величина прибутку 2000 року дорівнює
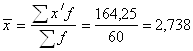 млн. грн.
млн. грн.
Висновки ІІ. Вибірка результативної ознаки – прибутку банків має наступні
характеристики:
Мода
– це величина, яка найчастіше зустрічається в даній сукупності. У варіаційному
ряді це буде варіант, що має найбільшу частоту.
Мода
прибутку досліджуємої вибірки банків= 2,33 млн. грн.
Медіана
– це варіант, що знаходиться в середині упорядкованого варіаційного ряду, тобто
ділить його на дві рівні частини. Медіана показує величину варіюючої ознаки,
якої досягла половина сукупності.
Медіана
прибутку досліджуємої вибірки банків = 2,59 млн. грн.
Середня
величина це показник, що характеризує типовий рівень варіюючої ознаки в
розрахунку на одиницю однорідної сукупності.
Середня
величина прибутку розрахована за формулою середньої зваженої і дорівнює = 2,738
млн. грн.
Характер різниця
між середньою величиною та характеристиками моди і медіани вибірки
результативної ознаки повторює характер відповідних різниць між середньою
величиною, модою та медіаною вибірки факторного признаку , тобто показники
ранжирувані за зростанням у порядку Мода-Медіана-Середньозважена величина. Це
свідчить про наявність суттєвих нерівномірностей кількісного розподілу банків
по гістограмам факторних та результативних ознак,
тобто підтверджується гіпотеза , що середня
величина для даної виборки є недостатньо характерна величина.
Для побудови
подальших висновків необхідне продовження статистичного аналізу.
ІІІ.
Обчислення показників варіації.
Завдання етапу 3.
За даними ряду розподілу побудованому в п. ІІ
обчислити:
—
розмах варіації;
—
середнє лінійне відхилення;
—
середнє квадратичне відхилення;
—
дисперсію;
—
коефіцієнт варіації.
Вихідні дані та розрахунки необхідних величин
для обчислення всіх показників варіації подати в робочій таблиці.
Розмах
варіації ![]() млн. грн., де xmax, xmin – максимальне та мінімальне значення ознаки.
млн. грн., де xmax, xmin – максимальне та мінімальне значення ознаки.
Середнє
лінійне відхилення обчислюється як частка від ділення суми всіх відхилень на їх
число[2]

(1)
Ступінь
варіації об’єктивно відображає показник середнього
квадрату відхилення (дисперсія). Його обчислюють як середню арифметичну з суми
квадратів відхилень окремих варіантів від їх середньої за формулою:

(2)
Корінь
квадратний із середнього квадрату відхилень варіантів від їх середньої (тобто
дисперсії) називається середнім квадратичним відхиленням:
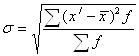
(3)
Дисперсія
і середнє квадратичне відхилення призначені для вимірювання варіації оцінки.
середнє квадратичне відхилення є мірилом надійності середньої. Чим менше
середнє квадратичне відхилення, тим повніше середня арифметична відображає всю
сукупність. Всі показники варіації – розмах варіації, середнє лінійне
відхилення, середній квадрат відхилення та середнє квадратичне відхилення
завжди виражаються в тих одиницях виміру, в яких виражені вихідні дані ряду та
середні. Всі вони є абсолютним виміром варіації. А це значить, що порівнювати
абсолютні показники варіації у варіаційних рядах різних явищ безпосередньо
неможливо. Для того, щоб забезпечити їх порівняння, потрібно обчислити
показники, які характеризували б варіацію, виражену в стандартних величинах,
наприклад, у процентах. Якщо порівняти середнє квадратичне відхилення з
середньою величиною, то і буде одержана ця стандартна величина. Одержаний
відносний показник називається коефіцієнтом варіації :
![]()
(4)
де ![]() — середнє арифметичне
— середнє арифметичне
інтервального ряду розподілу, f –
частота.
Коефіцієнт
варіації є в певній мірі критерієм типовості середньої. Якщо коефіцієнт дуже
великий, то це означає, що середня характеризує сукупність за ознакою, яка
суттєво змінюється у окремих одиниць.
Таблиця 5
Розрахунок показників варіації прибутку 2000 року
|
Групи одиниць сукупності за результативною ознакою |
Кількість одиниць (частота), f |
Середина інтервалу (варіанти), x/ |
|
|
|
|
| 0,2 – 1,95 | 21 | 1,075 | — 1,663 | 34,913 | 2,764 | 58,042 |
| 1,95 – 3,7 | 26 | 2,825 | 0,088 | 2,275 | 0,008 | 0,199 |
| 3,7 – 5,45 | 8 | 4,575 | 1,838 | 14,700 | 3,376 | 27,011 |
| 5,45 – 7,2 | 5 | 6,325 | 3,588 | 17,938 | 12,870 | 64,351 |
| Всього | 60 | – | 69,825 | 149,603 |
Таким чином,
середнє лінійне відхилення ![]() млн.
млн.
грн.
середнє квадратичне
відхилення ![]() млн. грн.
млн. грн.
дисперсія ![]() млн. грн.
млн. грн.
коефіцієнт варіації ![]() , якій дорівнює відношенню
, якій дорівнює відношенню
середньоквадратичного відхилення до середньозваженої величини прибутку по
досліджуваній виборці показників діяльності банків, розрахованій в розділі ІІ.
Висновки ІІІ. Додаткове
дослідження відносних статистичних характеристик вибірки результативної ознаки
(прибутку банку) для досліджуваної вибірки показало :
Розмах варіації
величин в вибірці прибутку банків дорівнює 7 млн. грн. Недоліком цього
показника є те, що він фіксує лише суму крайніх відхилень від середньої
величини прибутку в вибірці і зовсім не враховує відхилень всіх інших
варіантів прибутку від їх середньої величини . Узагальнюючу характеристику може
дати лише середня величина, зокрема середня із відхилень варіантів прибутку від
їх середньої величини прибутку.
Середнє лінійне
відхилення в вибірці прибутку дорівнює 1,164 млн. грн. Однак і цей показник не
завжди характеризує розсів варіантів.
Середнє квадратичне
відхилення вибірки прибутку від середньої величини дорівнює 1,58 млн. грн.
Середнє квадратичне відхилення велике, тобто середня арифметична не відображає
цілком всю сукупність.
Дисперсія вибірки
прибутку дорівнює 2,5 млн. грн.
Типовість середньої
величини прибутку для характеризування досліджувальної вибірки банків сумнівна,
оскільки має великі відхилення від середньої величини , які висвітлюються в
величині коефіцієнта варіації = 57,68%.
Згідно з [
] , cукупність вважається однорідною для
розподілів близьких до нормального, коли величина коефіцієнта варіації не
перевищує 33%.
Таким чином, за
даними статистичних досліджень , виконаних в пунктах І-ІІІ можна твердити, що
ми маємо справу з вибіркою, яка не підкоряється нормальному закону розподілу
відносно середньої величини , тобто вибірка банків, можливо, мала для
характеризування банківського процесу.
ІV. Статистичні методи вивчення взаємозв’язків між факторною
та результативною ознаками.
Завдання етапу 4.
На основі
розрахункових вихідних даних 2000 р. з табл. 1 виявити наявність і напрямок
кореляційного зв’язку між факторною і результативною ознаками, оцінити тісноту
зв’зку та перевірити його істотність (за рівнем істотності 0,05). Розрахувати
лінійне рівняння взаємозв’язку між факторною та
результативною ознаками.
Результативна
ознака – прибуток, факторна ознака – активи. Тобто
ПРИБУТОК = f (АКТИВИ)
Нехай X – активи, Y – прибуток.

Рис. 5. Графік кореляційного поля.
 |
Рівняння лінійного регресії має вигляд: y=a+bx, де
параметри a, b находимо з системи нормальних рівнянь[8]:
 |
(5)
(6)
Таблиця 6
Розрахункова таблиця.
| № п/п | X | Y | X*X | Y*Y | X*Y | Yx | (Yx-Ysr)^2 | (Y-Ysr)^2 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1 | 36,6 | 7,2 | 1339,56 | 51,84 | 263,52 | 3,59 | 1,03 | 21,42 |
| 2 | 60,3 | 2,4 | 3636,09 | 5,76 | 144,72 | 5,08 | 6,27 | 0,03 |
| 3 | 25,2 | 6,3 | 635,04 | 39,69 | 158,76 | 2,87 | 0,09 | 13,90 |
| 4 | 47,4 | 5,1 | 2246,76 | 26,01 | 241,74 | 4,26 | 2,87 | 6,39 |
| 5 | 61 | 4,3 | 3721 | 18,49 | 262,3 | 5,12 | 6,50 | 2,99 |
| 6 | 38,6 | 2,1 | 1489,96 | 4,41 | 81,06 | 3,71 | 1,30 | 0,22 |
| 7 | 36 | 6,4 | 1296 | 40,96 | 230,4 | 3,55 | 0,95 | 14,66 |
| 8 | 30,7 | 1,1 | 942,49 | 1,21 | 33,77 | 3,21 | 0,41 | 2,17 |
| 9 | 64,6 | 5,7 | 4173,16 | 32,49 | 368,22 | 5,35 | 7,70 | 9,79 |
| 10 | 35,1 | 2,2 | 1232,01 | 4,84 | 77,22 | 3,49 | 0,85 | 0,14 |
| 11 | 30,7 | 2,5 | 942,49 | 6,25 | 76,75 | 3,21 | 0,41 | 0,01 |
| 12 | 21,3 | 2,3 | 453,69 | 5,29 | 48,99 | 2,62 | 0,00 | 0,07 |
| 13 | 40 | 4,2 | 1600 | 17,64 | 168 | 3,80 | 1,51 | 2,65 |
| 14 | 38,7 | 3,7 | 1497,69 | 13,69 | 143,19 | 3,72 | 1,31 | 1,27 |
| 15 | 14,1 | 2,8 | 198,81 | 7,84 | 39,48 | 2,17 | 0,16 | 0,05 |
| 16 | 22,3 | 1,2 | 497,29 | 1,44 | 26,76 | 2,69 | 0,01 | 1,88 |
| 17 | 23,5 | 5 | 552,25 | 25 | 117,5 | 2,76 | 0,04 | 5,90 |
| 18 | 16,4 | 1,1 | 268,96 | 1,21 | 18,04 | 2,31 | 0,07 | 2,17 |
| 19 | 20,6 | 2,6 | 424,36 | 6,76 | 53,56 | 2,58 | 0,00 | 0,00 |
| 20 | 7,5 | 0,7 | 56,25 | 0,49 | 5,25 | 1,76 | 0,67 | 3,50 |
| 21 | 21,4 | 5,6 | 457,96 | 31,36 | 119,84 | 2,63 | 0,00 | 9,17 |
| 22 | 12,2 | 1,9 | 148,84 | 3,61 | 23,18 | 2,05 | 0,27 | 0,45 |
| 23 | 22 | 2,9 | 484 | 8,41 | 63,8 | 2,67 | 0,01 | 0,11 |
| 24 | 9,3 | 0,3 | 86,49 | 0,09 | 2,79 | 1,87 | 0,49 | 5,16 |
| 25 | 22,4 | 2,6 | 501,76 | 6,76 | 58,24 | 2,69 | 0,01 | 0,00 |
| 26 | 34,5 | 3,5 | 1190,25 | 12,25 | 120,75 | 3,45 | 0,78 | 0,86 |
| 27 | 13,4 | 2,2 | 179,56 | 4,84 | 29,48 | 2,13 | 0,20 | 0,14 |
| 28 | 10,2 | 1,5 | 104,04 | 2,25 | 15,3 | 1,92 | 0,42 | 1,15 |
| 29 | 13,9 | 2,5 | 193,21 | 6,25 | 34,75 | 2,16 | 0,17 | 0,01 |
| 30 | 26 | 2 | 676 | 4 | 52 | 2,92 | 0,12 | 0,33 |
| 31 | 31,8 | 3,6 | 1011,24 | 12,96 | 114,48 | 3,28 | 0,51 | 1,06 |
| 32 | 19,1 | 1,4 | 364,81 | 1,96 | 26,74 | 2,48 | 0,01 | 1,37 |
| 33 | 16,7 | 3,9 | 278,89 | 15,21 | 65,13 | 2,33 | 0,06 | 1,76 |
| 34 | 10,4 | 1,5 | 108,16 | 2,25 | 15,6 | 1,94 | 0,40 | 1,15 |
| 35 | 42 | 3,8 | 1764 | 14,44 | 159,6 | 3,93 | 1,83 | 1,51 |
| 36 | 6,8 | 0,9 | 46,24 | 0,81 | 6,12 | 1,71 | 0,74 | 2,79 |
| 37 | 10,9 | 3,4 | 118,81 | 11,56 | 37,06 | 1,97 | 0,36 | 0,69 |
| 38 | 8 | 0,4 | 64 | 0,16 | 3,2 | 1,79 | 0,62 | 4,72 |
| 39 | 14,3 | 3,7 | 204,49 | 13,69 | 52,91 | 2,18 | 0,15 | 1,27 |
| 40 | 20,8 | 0,9 | 432,64 | 0,81 | 18,72 | 2,59 | 0,00 | 2,79 |
| 41 | 12,5 | 2,3 | 156,25 | 5,29 | 28,75 | 2,07 | 0,25 | 0,07 |
| 42 | 10,5 | 1 | 110,25 | 1 | 10,5 | 1,94 | 0,39 | 2,47 |
| 43 | 12,5 | 3,3 | 156,25 | 10,89 | 41,25 | 2,07 | 0,25 | 0,53 |
| 44 | 4,5 | 0,4 | 20,25 | 0,16 | 1,8 | 1,57 | 1,01 | 4,72 |
| 45 | 19 | 2 | 361 | 4 | 38 | 2,48 | 0,01 | 0,33 |
| 46 | 9,2 | 1,2 | 84,64 | 1,44 | 11,04 | 1,86 | 0,50 | 1,88 |
| 47 | 8,3 | 2 | 68,89 | 4 | 16,6 | 1,81 | 0,59 | 0,33 |
| 48 | 3 | 5 | 9 | 25 | 15 | 1,47 | 1,21 | 5,90 |
| 49 | 10,7 | 4 | 114,49 | 16 | 42,8 | 1,96 | 0,38 | 2,04 |
| 50 | 5,7 | 0,2 | 32,49 | 0,04 | 1,14 | 1,64 | 0,86 | 5,62 |
| Продовження табл.6 | ||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 51 | 11,9 | 2,3 | 141,61 | 5,29 | 27,37 | 2,03 | 0,29 | 0,07 |
| 52 | 9 | 0,4 | 81 | 0,16 | 3,6 | 1,85 | 0,52 | 4,72 |
| 53 | 10,4 | 2,1 | 108,16 | 4,41 | 21,84 | 1,94 | 0,40 | 0,22 |
| 54 | 10,8 | 0,9 | 116,64 | 0,81 | 9,72 | 1,96 | 0,37 | 2,79 |
| 55 | 12,2 | 2,7 | 148,84 | 7,29 | 32,94 | 2,05 | 0,27 | 0,02 |
| 56 | 5,2 | 0,6 | 27,04 | 0,36 | 3,12 | 1,61 | 0,92 | 3,89 |
| 57 | 11,2 | 2,3 | 125,44 | 5,29 | 25,76 | 1,99 | 0,34 | 0,07 |
| 58 | 9,8 | 0,3 | 96,04 | 0,09 | 2,94 | 1,90 | 0,45 | 5,16 |
| 59 | 9,8 | 3,4 | 96,04 | 11,56 | 33,32 | 1,90 | 0,45 | 0,69 |
| 60 | 5,2 | 0,5 | 27,04 | 0,25 | 2,6 | 1,61 | 0,92 | 4,29 |
| Сума | 1228,1 | 154,3 | 37700,61 | 568,31 | 3949,01 | 154,25 | 49,71 | 171,50 |
| X | Y | X*X | Y*Y | X*Y |
Yx |
(Yx-Ysr)2 |
(Y-Ysr)2 |
|
Yx — теоретичні значення результативної ознаки, які розраховуються за
отриманим лінійним рівнянням регресії; Ysr – середня величина змінної Y.
 , тобто y=1,2834+0,0629x
, тобто y=1,2834+0,0629x
Знайдемо
коефіцієнт детермінації і перевіримо адекватність отриманого рівняння лінійної
регресії за критерієм Фішера. Коефіцієнт детермінації визначається наступним
чином:

Коефіцієнт детермінації характеризує ту частину
варіації результативної ознаки, яка відповідає лінійному рівнянню регресії.
При виконанні процедури перевірки значущості
коефіцієнта детермінації висувається нульова гіпотеза H0 проти
альтернативи H1, котра заключаються в наступному:
H0: істотної різниці між вибірковим коефіцієнтом
детермінації та коефіцієнтом детермінації генеральної сукупності не існує. Ця
гіпотеза рівносильна гіпотезі H0: b=0, тобто змінні X
не впливають суттєво на залежну змінну Y. Для оцінки значущості коефіцієнта
детермінації використовується статистика:
![]()
що має F-розподіл Фішера з f1=1 та f2=n — 2=60-2=58
ступенями вільності.
Значення статистики порівнюється з критичним значенням цієї статистики,
знайденим за таблицею при заданому рівні значущості a=0,05 та відповідному числі
ступенів вільності. Якщо F>F1,n — 2,a , то обчислений коефіцієнт
детермінації істотно відрізняється від нуля. Цей висновок забезпечується з
ймовірністю 1-a.
Задамося рівнем значущості a=0,05. Кількість ступенів вільності
наступна: f1=1, f2=58. По таблиці находимо
критичне значення F1,58,0.05 = 4,03.
Так як F>F1,58,0.05 (23,7 > 4,03), то робимо висновок, що
включені в регресію змінні достатньо пояснюють залежну змінну.

Рис. 6. Графік теоретичної лінійної
регресії.
Індекс кореляції: R= ![]() =0,54. Індекс кореляції
=0,54. Індекс кореляції
вимірює щільність зв’язку і не показує її напрямок.
Лінійний коефіцієнт
кореляції обчислюється за формулою[9]:

Лінійний коефіцієнт кореляції чим ближче до 1,
тим тісніше зв’язок. Знак коефіцієнта вказує напрямок зв’язку:
знак “+” відповідає прямій залежності, знак “-“ – оберненій залежності.
Висновки ІV.
Аналіз кореляційного зв ‘ язку між
факторною(активами) та результативною(прибутком) показниками досліджувальної
вибірки показників діяльності банків дає наступні результати :
1. Кореляційний зв ‘ язок для
лінійної регресії має наступне рівняння та відносні характеристики :
Рівняння лінійної
регресії y=1,2834+0,0629x.
Коефіцієнт
детермінації дорівнює 0,29.
За критерієм Фішера
зв’язок знайдено істотним.
Індекс кореляції
дорівнює 0,54.
Лінійний коефіцієнт
кореляції дорівнює 0,54 (сила зв’язка – середня).
Напрямок зв’язку –
додатній.
2. Оскільки
отриманий коефіцієнт детермінації дорівнює 0,29, то тільки 29% варіації
прибутку банків пов’язано з варіацією активів банків, а 71% варіації припадає
на решту факторів. Тобто зв’язок не є щільним, оскільки економічно прибуток
банків залежить не тільки від їх активів, а ще від доходності цих активів ,
яка залежить від їх структури, та собівартості послуг для кожного банку.
Отриманий результат є об’єктивним, оскільки прибуток банку дорівнює різниці між
доходами від застосування активів та собівартістю (витратами) банків при
здійсненні різних за масштабами та рівнем витрат доходних операцій.
V. Обчислення характеристик рядів динаміки
Завдання
етапу 5.
На основі даних про активи банка за 9-12 місяці 1996-2000 рр. (табл. 2)
визначити:
1. Ланцюгові та
базисні (по відношенню до 1996 р.) показники динаміки активів за 9, 10, 11, 12
місяці окремо:
—
абсолютний
приріст;
—
темп
зростання і темп приросту;
—
абсолютне
значення 1% приросту.
Результати
розрахунків подати у 4 таблицях. Перевірити взаємозв’язок ланцюго-вих
аналітичних показників ряду динаміки і базисних.
2. Середні
значення вище перелічених показників:
—
середній
рівень;
—
середній
абсолютний приріст;
—
середній
темп зростання;
—
середній
темп приросту.
3. Індекси
сезонності, що дають характеристику внутрішньорічній динаміці і побудувати
графік сезонної хвилі активів банку.
У процесі аналізу рядів
динаміки обчислюють і використовують наступні аналітичні показники динаміки: абсолютний
приріст, темп зростання, темп приросту і абсолютне
значення одного проценту приросту. Обчислення цих показників грунтується на
абсолютному або відносному зіставленні між собою рівнів ряду динаміки. Рівень,
який зіставляється, називають звітним, а рівень, з яким зіставляють інші
рівні – базисним. За базу зіставлення приймають початковий (перший)
рівень ряду динаміки. Якщо кожний наступний рівень зіставляють з попереднім, то
отримують ланцюгові показники динаміки, а якщо кожний наступний рівень
зіставляють з рівнем, що взятий за базу зіставлення, то одержані показники
називають базисними [1] – [9].
Абсолютний приріст
обчислюється як різниця між звітним і базисним рівнями і показує, на скільки
одиниць підвищився чи зменшився рівень порівняно з базисним за певний період
часу. Він виражається в тих же одиницях виміру, що й рівні динаміки.
![]() або
або ![]() (7)
(7)
де yi – звітний рівень ряду динаміки; yi — 1 – попередній рівень ряду динаміки;
y1 – початковий рівень ряду динаміки.
Темп зростання обчислюється як
відношення зіставлюваного рівня з рівнем, прийнятого за базу зіставлення, і
показує, у скільки разів (процентів) зрівнюваний рівень більший чи менший від
базисного.
![]() або
або ![]()
(8)
Темп приросту визначається як
відношення абсолютного приросту до абсолютного попереднього або початкового
рівня і показує, на скільки процентів порівнювальний рівень більший або менший
від рівня, взятого за базу порівняння.
![]() або
або ![]()
(9)
Абсолютне значення одного проценту
приросту визначається шляхом ділення абсолютного приросту на темп приросту
за один і той же період.
![]()
(10)
Середній абсолютний приріст
визначається як середня арифметична проста з ланцюгових приростів за певні
періоди і показує, на скільки одиниць в середньому змінився рівень порівняно з
попереднім.
![]()
(11)
Середній темп зростання розраховується за формулою
середньої геометричної для ланцюгових темпів зростання:
![]() ,
,
або (12)
![]()
![]()
Середній темп приросту визначається як різниця між
середнім темпом зростання та одиницею (якщо середній темп зростання вигляді
коефіцієнта), бо між середнім темпом зростання та 100% (якщо він у процентах)
![]() (у вигляді коефіцієнтів);
(у вигляді коефіцієнтів);
(13)
![]() (у вигляді
(у вигляді
процентів). (14)
Середній темп приросту показує, на скільки
процентів збільшився або зменшився рівень порівняно з попереднім в середньому
за одиницю часу.
Середній рівень досліджуємого моментного ряду
динаміки зміни показників у часі розраховується за формулою середньохронологічної
(n- кількість членів
хронологічного ряду динаміки показників), згідно з якою крайні члени
враховуються в величинах 50% від свого значення :

(15)
В таблиці 7
наведені результати розрахунків по формулам (7) –(15)
параметрів часового ряду динаміки показників активів
банку за дев ‘ яті місяці.
Розрахунки виконані з використанням таблиць EXCEL — 2000 з послідовним програмуванням ячеєк
вищенаведеними формулами . Середні характеристики ряду динаміки розрахоівані
—
середньохронологічний
рівень інтервального ряду динаміки активів дорівнює по (15) :
![]()

![]() — середньоарифметичне
— середньоарифметичне
значення абсолютного ланцюгового прирісту активів дорівнює ( та має сенс для
характеризування ряду між його крайніми значеннями, що підтверджується
порівненням з базисними значеннями абсолютного прирісту в табл.7, які вказують
на проміжні накоплені характеристики приросту значень членів ряду динаміки
відносно початкового-базисного рівня 1996 року):
![]()
![]()

Середній темп зростання активів банку та
середній коефіцієнт росту активів банку розраховуємо за формулою
середньогеометричної величини (12) :
![]() або 100,2528%
або 100,2528%
Середній темп приросту активів банку
розраховуємо за формулою (14) як :
![]()
Середня величина абсолютного приросту активів
на 1% приросту розраховується як середньоарифметична значень , розрахованих за
формулою(10) в табл.7 для всіх моментів часу.
Результати розрахунків наведені в табл.
7,8,9,10.
Таблиця 7
Розрахунок показників динаміки активів за 9-ті місяці
1996-2000 рр.
| Роки | 1996 | 1997 | 1998 | 1999 | 2000 | |||||||
| Вартість активів, млн. грн. |
31,52 | 32,99 | 32,44 | 34,59 | 31,84 | |||||||
| Найменування показника | 1996 | 1997 | 1998 | 1999 | 2000 | |||||||
| Абсолютний | ланцюговий | — | 1,47 | — 0,55 | 2,15 | — 2,75 | ||||||
| приріст, млн. грн. |
базисний 1996 | — | 1,47 | 0,92 | 3,07 | 0,32 | ||||||
| Коефіцієнт | ланцюговий | — | 1,05 | 0,98 | 1,07 | 0,92 | ||||||
| росту | базисний 1996 | — | 1,05 | 1,03 | 1,10 | 1,01 | ||||||
| (перевірка: базис-ний індекс дорінює множині ланцюго-вих індексів) |
=1,05*0,98 =1,03 | =1,05*0,98*1,07 =1,10 | =1,05*0,98*1,07*0,92 = 1,01 | |||||||||
| Темп | ланцюговий | — | 104,66 | 98,33 | 106,63 | 92,05 | ||||||
| зростання, % | базисний 1996 | — | 104,66 | 102,92 | 109,74 | 101,02 | ||||||
| Темп | ланцюговий | — | 4,66 | — 1,67 | 6,63 | — 7,95 | ||||||
| приросту, % | базисний 1996 | — | 4,66 | 2,92 | 9,74 | 1,02 | ||||||
| Абсолютне зна- | ланцюговий | — | 0,32 | 0,33 | 0,32 | 0,35 | ||||||
| чення 1% прирісту | базисний 1996 | — | 0,32 | 0,32 | 0,32 | 0,32 | ||||||
| Середній рівень моментного хронологічного ряду | 32,925 | млн. грн. | ||||||||||
| Середньорічний ланцюговий абсолютний приріст за змінною базою | 0,08 | млн. грн. | /на рік | |||||||||
| Середній ланцюговий коефіцієнт росту за змінною базою | 1,002528 | |||||||||||
| Середній ланцюговий темп росту за змінною базою | 100,2528 | % | ||||||||||
| Середній ланцюговий темп приросту за змінною базою | 0,252847 | % | ||||||||||
| Середня ланцюгова величина абс.значення 1% прирісту | 0,316397 | млн. грн. | /на 1% | |||||||||
Таблиця 8
Розрахунок показників динаміки активів за 10-ті місяці
1996-2000 рр.
| Роки | 1996 | 1997 | 1998 | 1999 | 2000 | |||||||
| Вартість активів, млн. грн. |
30,52 | 31,10 | 31,80 | 34,95 | 32,57 | |||||||
| Найменування показника | 1996 | 1997 | 1998 | 1999 | 2000 | |||||||
| Абсолютний | ланцюговий | — | 0,58 | 0,70 | 3,15 | — 2,38 | ||||||
| приріст, млн. грн. |
базисний 1996 | — | 0,58 | 1,28 | 4,43 | 2,05 | ||||||
| Коефіцієнт | ланцюговий | — | 1,02 | 1,02 | 1,10 | 0,93 | ||||||
| роста | базисний 1996 | — | 1,02 | 1,04 | 1,15 | 1,07 | ||||||
| Темп | ланцюговий | — | 101,90 | 102,25 | 109,91 | 93,19 | ||||||
| зростання, % | базисний 1996 | — | 101,90 | 104,19 | 114,52 | 106,72 | ||||||
| Темп | ланцюговий | — | 1,90 | 2,25 | 9,91 | — 6,81 | ||||||
| прирісту, % | базисний 1996 | — | 1,90 | 4,19 | 14,52 | 6,72 | ||||||
| Абсолютне зна- | ланцюговий | — | 0,31 | 0,31 | 0,32 | 0,35 | ||||||
| чення 1% прирісту | базисний 1996 | — | 0,31 | 0,31 | 0,31 | 0,31 | ||||||
| Середній рівень моментного хронологічного ряду | 32,349 | млн. грн. | ||||||||||
| Середньорічний ланцюговий абсолютний приріст за змінною базою | 0,5125 | млн. грн. | ||||||||||
| Середній ланцюговий коефіцієнт росту за змінною базою | 1,016385 | |||||||||||
| Середній ланцюговий темп росту за змінною базою | 101,6385 | % | ||||||||||
| Середній ланцюговий темп приросту за змінною базою | 1,638514 | % | ||||||||||
| Середня ланцюгова величина абс.значення 1% прирісту | 0,312783 | млн. грн. | ||||||||||
Таблиця 9
Розрахунок показників динаміки активів за 11-ті місяці
1996-2000 рр.
| Роки | 1996 | 1997 | 1998 | 1999 | 2000 | |||||||
| Вартість активів, млн. грн. |
30,85 | 30,79 | 35,34 | 36,01 | 31,84 | |||||||
| Найменування показника | 1996 | 1997 | 1998 | 1999 | 2000 | |||||||
| Абсолютний | ланцюговий | — | — 0,06 | 4,55 | 0,67 | — 4,17 | ||||||
| приріст, млн. грн. | базисний 1996 | — | — 0,06 | 4,49 | 5,16 | 0,99 | ||||||
| Коефіцієнт | ланцюговий | — | 1,00 | 1,15 | 1,02 | 0,88 | ||||||
| роста | базисний 1996 | — | 1,00 | 1,15 | 1,17 | 1,03 | ||||||
| Темп | ланцюговий | — | 99,81 | 114,78 | 101,90 | 88,42 | ||||||
| зростання, % | базисний 1996 | — | 99,81 | 114,55 | 116,73 | 103,21 | ||||||
| Темп | ланцюговий | — | — 0,19 | 14,78 | 1,90 | — 11,58 | ||||||
| приросту, % | базисний 1996 | — | — 0,19 | 14,55 | 16,73 | 3,21 | ||||||
| Абсолютне зна- | ланцюговий | — | 0,31 | 0,31 | 0,35 | 0,36 | ||||||
| чення 1% прирісту | базисний 1996 | — | 0,31 | 0,31 | 0,31 | 0,31 | ||||||
| Середній рівень моментного хронологічного ряду | 33,371 | млн. грн. | ||||||||||
| Середньорічний ланцюговий абсолютний приріст за змінною базою | 0,2475 | млн. грн. | ||||||||||
| Середній ланцюговий коефіцієнт росту за змінною базою | 1,007928 | |||||||||||
| Середній ланцюговий темп росту за змінною базою | 100,7928 | % | ||||||||||
| Середній ланцюговий темп приросту за змінною базою | 0,792791 | % | ||||||||||
| Середня ланцюгова величина абс.значення 1% прирісту | 0,312188 | млн. грн. | ||||||||||
Таблиця 10
Розрахунок показників динаміки активів за 12-ті місяці
1996-2000 рр.
| Роки | 1996 | 1997 | 1998 | 1999 | 2000 |
| Вартість активів, млн. грн. |
33,54 | 31,42 | 32,12 | 35,30 | 36,60 |
| Найменування показника | 1996 | 1997 | 1998 | 1999 | 2000 | |
| Абсолютний | ланцюговий | — | — 2,12 | 0,70 | 3,18 | 1,30 |
| приріст, млн. грн. |
базисний 1996 | — | — 2,12 | — 1,42 | 1,76 | 3,06 |
| Коефіцієнт | ланцюговий | — | 0,94 | 1,02 | 1,10 | 1,04 |
| роста | базисний 1996 | — | 0,94 | 0,96 | 1,05 | 1,09 |
| Темп | ланцюговий | — | 93,68 | 102,23 | 109,90 | 103,68 |
| зростання, % | базисний 1996 | — | 93,68 | 95,77 | 105,25 | 109,12 |
| Темп | ланцюговий | — | — 6,32 | 2,23 | 9,90 | 3,68 |
| приросту, % | базисний 1996 | — | — 6,32 | — 4,23 | 5,25 | 9,12 |
| Абсолютне зна- | ланцюговий | — | 0,34 | 0,31 | 0,32 | 0,35 |
| чення 1% прирісту | базисний 1996 | — | 0,34 | 0,34 | 0,34 | 0,34 |
| Середній рівень моментного хронологічного ряду | 33,477 | млн. грн. | ||||
| Середньорічний ланцюговий абсолютний приріст за змінною базою | 0,765 | млн. грн. | ||||
| Середній ланцюговий коефіцієнт росту за змінною базою | 1,022067 | |||||
| Середній ланцюговий темп росту за змінною базою | 102,2067 | % | ||||
| Середній ланцюговий темп приросту за змінною базою | 2,206733 | % | ||||
| Середня ланцюгова величина абс.значення 1% прирісту | 0,346666 | млн. грн. | ||||
Отримані результати запишемо в табл.11 :
Таблиця 11
Характеристики рядів динаміки активів банку у 9-12
місяцях 1996 –2000 років
|
Місяці 1996-2000 |
Середній рівень моментного ряду, млн.грн |
Середній абсолютний приріст, млн.грн./рік |
Середній коефіцієнт росту |
Середній темп росту, % |
Середній темп приросту,% |
Середня величина абс. значення 1% при-росту, млн.грн./1% |
| 9-ті | 32,925 | 0,08 | 1,002 | 100,2 | 0,253 | 0,316 |
| 10-ті | 32,349 | 0,513 | 1,016 | 101,6 | 1,639 | 0,313 |
| 11-ті | 33,371 | 0,248 | 1,008 | 100,8 | 0,793 | 0,312 |
| 12-ті | 33,477 | 0,765 | 1,022 | 102,2 | 2,207 | 0,347 |
Аналіз результатів табл.11 показує , що активи банку з 9 по 12 місяць
мають тенденцію нарощування кожного року. Для аналізу цього явища необхідно
провести сезонний аналіз активів банку за місяцями року. Динаміка приросту
активів в рядах 9-12 місяців за період 1996-2000 років позитивна, тобто є
нарощування активів з темпом приросту за 12 місяць +2,2 % , але темп приросту
за місяцями різний. Картина неоднорідності часових рядів досліджувальної
виборки активів банку наведена на рис. 7.

Класична модель сезонної хвилі (для активів) має
вигляд наступного рівняння:
![]()
(16)
Параметри рівняння визначаються за формулами:
![]()
![]()
![]()
(17)
Для розрахунків параметрів рівняння використана наступна допоміжна
таблиця 12 в якій розраховані суми для розрахунків коефіцієнтів за формулами
(17) :
Таблиця 12
Розрахунок параметрів моделі сезонної хвилі
| Місяць | Вартість активів за роками | Середні | ||||||||||
| 1996 | 1997 | 1998 | 1999 | 2000 | рівні, y | t | cos t | sin t | y*cost | y*sint | y(t) за формулою | |
| 1 | 36,89 | 27,96 | 30,52 | 37,07 | 37,33 | 33,95 | 0 | 1,00 | 0,00 | 33,95 | 0,00 | 33,48 |
| 2 | 32,86 | 29,85 | 29,87 | 36,36 | 36,97 | 33,18 | (1/6)p | 0,87 | 0,50 | 28,74 | 16,59 | 33,41 |
| 3 | 31,86 | 30,79 | 30,84 | 35,65 | 35,50 | 32,93 | (1/3)p | 0,50 | 0,87 | 16,46 | 28,52 | 33,19 |
| 4 | 31,52 | 30,16 | 30,20 | 36,01 | 35,87 | 32,75 | (1/2)p | 0,00 | 1,00 | 0,00 | 32,75 | 32,87 |
| 5 | 30,52 | 30,47 | 31,48 | 34,95 | 35,14 | 32,51 | (2/3)p | — 0,50 | 0,87 | — 16,26 | 28,16 | 32,55 |
| 6 | 30,18 | 31,10 | 33,73 | 33,54 | 33,31 | 32,37 | (5/6)p | — 0,87 | 0,50 | — 28,03 | 16,19 | 32,31 |
| 7 | 29,51 | 31,73 | 34,69 | 34,59 | 32,57 | 32,62 | p | — 1,00 | 0,00 | — 32,62 | 0,00 | 32,21 |
| 8 | 29,85 | 32,05 | 32,77 | 33,89 | 32,21 | 32,15 | (7/6)p | — 0,87 | — 0,50 | — 27,84 | — 16,08 | 32,28 |
| 9 | 31,52 | 32,99 | 32,44 | 34,59 | 31,84 | 32,68 | (4/3)p | — 0,50 | — 0,87 | — 16,34 | — 28,30 | 32,50 |
| 10 | 30,52 | 31,10 | 31,80 | 34,95 | 32,57 | 32,19 | (3/2)p | 0,00 | — 1,00 | 0,00 | — 32,19 | 32,81 |
| 11 | 30,85 | 30,79 | 35,34 | 36,01 | 31,84 | 32,96 | (5/3)p | 0,50 | — 0,87 | 16,48 | — 28,55 | 33,13 |
| 12 | 33,54 | 31,42 | 32,12 | 35,30 | 36,60 | 33,80 | (11/6)p | 0,87 | — 0,50 | 29,27 | — 16,90 | 33,38 |
| Всього | 394,09 | 3,81 | 0,19 | 394,09 | ||||||||
Параметри рівнянь (17) , розраховані за даними
проміжної табл. 12 наступні:
![]()
![]()
![]()
Таким
чином, згідно формулі (16) — Модель сезонної хвилі активів банку має приймає
вигляд:
![]()
Розрахуємо індекси
сезонності: 1) визначимо середні рівні для кожного місяця; 2) визначимо
загальну середню за весь період (табл.13). Загальна середня розраховується як
середньозважена величина середніх рівніх активів за і-тими місяцями за
1996-2000 роки(наведеними в табл.13-останній стовпчик), зваженими на кількість днів
у місяці та нормованими на 365 днів(рік): ![]()
Таблиця 13
Результати
розрахунків
| Місяць | Вартість активів за роками в млн.грн. | Індекси сезонності –відношення середніх активів місяця до загальної середньої |
Середні рівні активів в млн.грн. за i-й місяць 1996-2000 |
||||
| 1996 | 1997 | 1998 | 1999 | 2000 | |||
| 1 | 36,89 | 27,96 | 30,52 | 37,07 | 37,33 |
33,95/32,84 = 1,0338 |
33,95 |
| 2 | 32,86 | 29,85 | 29,87 | 36,36 | 36,97 |
1,0104 |
33,18 |
| 3 | 31,86 | 30,79 | 30,84 | 35,65 | 35,50 |
1,0026 |
32,93 |
| 4 | 31,52 | 30,16 | 30,20 | 36,01 | 35,87 |
0,9972 |
32,75 |
| 5 | 30,52 | 30,47 | 31,48 | 34,95 | 35,14 |
0,9899 |
32,51 |
| 6 | 30,18 | 31,10 | 33,73 | 33,54 | 33,31 |
0,9857 |
32,37 |
| 7 | 29,51 | 31,73 | 34,69 | 34,59 | 32,57 |
0,9933 |
32,62 |
| 8 | 29,85 | 32,05 | 32,77 | 33,89 | 32,21 |
32,15/32,84 = 0,9790 |
32,15 |
| 9 | 31,52 | 32,99 | 32,44 | 34,59 | 31,84 |
0,9950 |
32,68 |
| 10 | 30,52 | 31,10 | 31,80 | 34,95 | 32,57 |
0,9801 |
32,19 |
| 11 | 30,85 | 30,79 | 35,34 | 36,01 | 31,84 |
1,0038 |
32,96 |
| 12 | 33,54 | 31,42 | 32,12 | 35,30 | 36,60 |
1,0290 |
33,80 |

Рис. 8. Модель сезонної хвилі
активів банку.
VI. Розрахунок
індексів
Завдання
етапу 6.
За даними
перших 5 банків 2000 року з таблиці 1 розрахувати:
1. Середній рівень
рентабельності активів в базовому і звітному періодах.
2. Індивідуальні
індекси рентабельності активів.
3. Загальні
індекси: а) прибутку; б) рентабельності; в) активів.
4. Динаміку
середнього рівня рентабельності активів (змінного, фіксованого складу та
структурних зрушень).
Таблица 14
| Банки |
Рентабельність =(Прибуток/Активи)*100% |
|||||
| Прибуток, млн. грн. |
Активи, млн. грн. |
|||||
| базовий період, 1999 |
звітний період, 2000 |
базовий період, 1999 |
звітний період, 2000 |
базовий період, 1999 |
звітний період, 2000 |
|
| 1 | 7 | 7,2 | 35,3 | 36,6 | 19,8% | 19,7% |
| 2 | 2,5 | 2,4 | 60,2 | 60,3 | 4,0% | 4,0% |
| 3 | 6,2 | 6,3 | 23,6 | 25,2 | 26,3% | 25% |
| 4 | 5 | 5,1 | 45,5 | 47,4 | 11,0% | 10,8% |
| 5 | 4,1 | 4,3 | 64 | 61 | 6,4% | 7% |
| Всього | 24,8 | 25,3 | 228,6 | 230,5 | ||
Індивідуальні
індекси рентабельності активів( відношення рентабельностей активів з табл.14 у
звітному 2000 році до базового 1999 року) для визначених 5 банків становлять:
![]()
![]()
![]()
![]()
![]()
Отримні
результати свідчать, що в звітному періоді вбанку №5 відносний рівень
рентабельністі зріс на +0,09 (+9%,) , в банку № 2 – зостався на тому ж рівні, а
в банках № 1, 4, 3 , відповідно, впав на –1%, — 2% та – 5%
Загальний індекси сумарних значень прибутку,активів та рентабельності
по сумарній виборці 5 банків у звітному році відносно базового(1999) року
розраховується як відношення :

(18)

(19)

(20)
Загальний індекс
прибутку по сумарній виборці 5 банків(табл.14) у звітному році відносно
базового(1999) року розраховується як відношення :
![]() або 102%
або 102%
Загальний індекс
активів по сумарній виборці 5 банків(табл.14) у звітному році відносно
базового(1999) року розраховується як відношення : ![]() або 100,8%
або 100,8%
Загальний індекс
рентабельності по сумарній виборці 5 банків(табл.14) у звітному році відносно
базового(1999) року розраховується як відношення :  %
%
Зміни
середнього рівня рентабельності активів у звітному періоді(1-2000 р.) відносно
базового(0 –1999 р.) визвані наступними чинниками – індексами фіксованого
складу та індексами структурних зрушень:
Індекс змінного
складу  або
або
101%
Індекс фіксованого
складу  або 102%
або 102%
Індекс структурних
зрушень  або 99%
або 99%
Контрольне
співвідношення індексів наступне :
![]()
Висновки VI:
Згідно з отриманими результатами індекс
змінного составу середньої рентабельності по виборці сумарних результатів по
5-ти банкам у звітному році становить 1,012 , або рентабельність зросла на 1,2
%, при цьому :
—
за рахунок зростання
власне прибутку індекс зростання рентабельності становить 1,02 , або зріст на
+2%;
—
за рахунок зростання
активів індекс падіння рентабельності становить 0,99,
або падіння на — 1%.
ВИСНОВКИ
Згідно з проведеною статистичною обробкою даних по виборці 60
банків
можна зробити
наступні висновки відносно отриманих часткових висновків за зробленими етапами
статистичної обробки :
1.
Застосування методу розподілу індексів агрегатного, фіксованого складу та
структурних зрушень дозволяє констатувати, що у звітному періоді зростання
рентабельності активів по групі банків відбулося на 1,2 % , при цьому за
рахунок прибутку зростання становить 2%, а за рахунок збільшення активів –
падіння становить –1%.
2. Побудована сезонна хвиля активів
банку, яка показує зниження активів у літньому періоду, коли зменшуються
заощаджені вклади населення при їх витратах на відпочинку.
3. Аналіз функціонального зв ‘ язку
активів (фактор) та прибутку (результат) показав наявність лінійної форми
регресії — рівняння лінійної регресії y=1,2834+0,0629x. Коефіцієнт
детермінації дорівнює 0,29. За критерієм Фішера зв’язок знайдено істотним.
Індекс кореляції дорівнює 0,54. Лінійний коефіцієнт кореляції дорівнює 0,54
(сила зв’язка – середня). Напрямок зв’язку – додатній.
Оскільки отриманий
коефіцієнт детермінації дорівнює 0,29, то тільки 29% варіації прибутку банків
пов’язано з варіацією активів банків, а 71% варіації припадає на решту
факторів. Тобто зв’язок не є щільним, оскільки економічно прибуток банків
залежить не тільки від їх активів, а ще від доходності цих активів , яка
залежить від їх структури, та собівартості послуг для кожного банку. Отриманий
результат є об’єктивним, оскільки прибуток банку дорівнює різниці між доходами
від застосування активів та собівартістю (витратами) банків при здійсненні
різних за масштабами та рівнем витрат доходних операцій.
4. Гістограмно-інтервальний аналіз
виборки даних показує , що серед вибраних 60 банків , основна маса має
невеликий капітал, який виробляє відповідний невеликий прибуток з аналогічним
розподілом.
Перелік використанної
літератури
1. Вашків П.Г., Пастер П.І.,
Сторожук В.П., Ткач Є.І. Статистика підприємництва:
Навч. посібник – К.:
Слобожанщина, 1999.
2. Двірник В.М. Статистичне вивчення зв’язків соціально-економічних
явищ:
конспект лекцій. – Дніпропетровськ: ДАУБП, 1999.
3. Двірник В.М.
Статистичні індекси в економічних дослідженнях. Дніпропет-
ровськ: ДАУБП,
1998.
4. Елисеева И.И., Юзбашев М.М. Общая
теория статистики: Учебник. – 4-е изд.,
перераб и доп. – М: Финансы и
статистика, 1999.
5. Ефимова М.Р., Ганченко О.И., Петрова
Е.В. Практикум по общей теории
статистики. М: Финансы и
статистика, 2000.
6. Ефимова М.Р., Петрова Е.В., Румянцев
В.Н. и др. Общая теория статистики:
Учебник. – М: Инфра-М, 1998.
7. Общая теория статистики: Учебник. / Под ред. А.А.
Спирина, О.Э. Башиной. –
5-е изд., доп. и перераб. – М.:
Финансы и статистика, 1999.
8. Статистика.
За ред. А.В. Головача, А.М. Єріної, О.В. Козирєва. – К.: Вища
школа, 1993.
9. Экономическая статистика: Метод. разработка / Сост. В.С.
Федоренко – К.:
МАУП,1999.
